I was inspired by the thought “How could I get a swarm of robots to split into groups in order to move to different locations?”. Ideally, this means we find a way to allow a network of robots to split into $K$ equal-sized groups, then move to a location assigned to that group. For example, a swarm of robots might need to split into three groups to explore three areas. Beyond simple exploration, the same approach could be useful for assigning $K$ targets, distributing $K$ tasks, or executing a distributed computation with $K$ parallel components.
We assume that we always have a connected graph, that nodes have unique IDs (at least locally, enough to uniquely address neighbors), and that everyone can keep track of their neighbors. One node will initiate the partitioning process with a flood-fill announcement, the partitioning process will occur, and the nodes should make their way to their groups location on screen.
Let’s start with the naive implementation and see where it takes us.
Random assignment
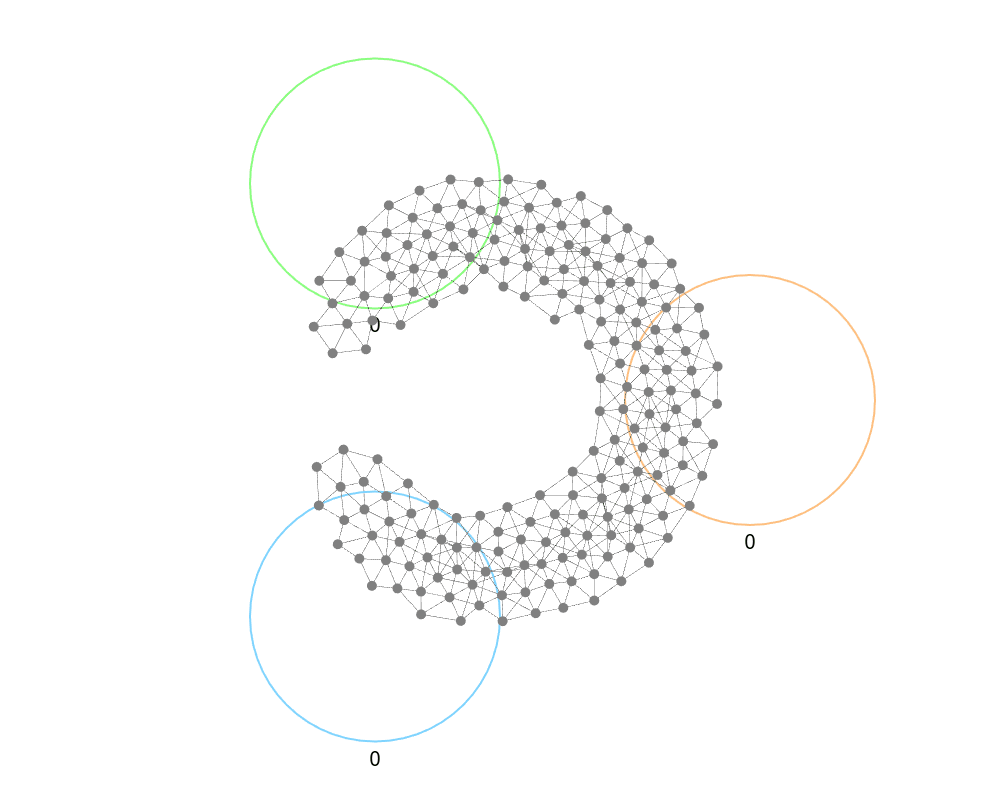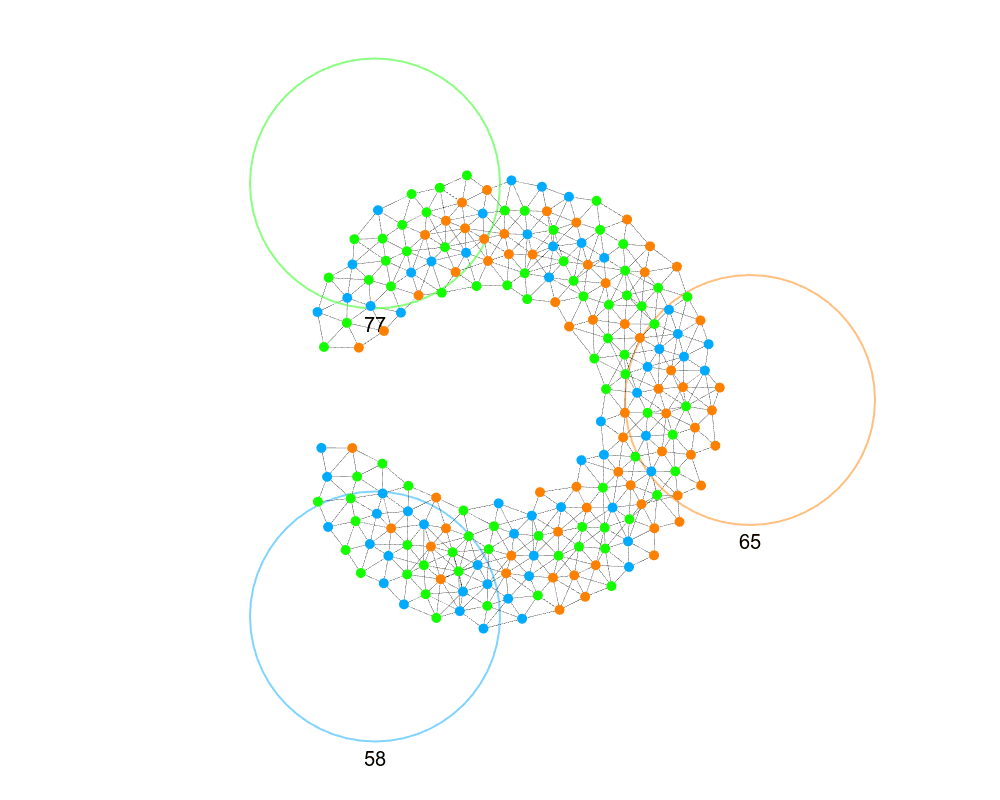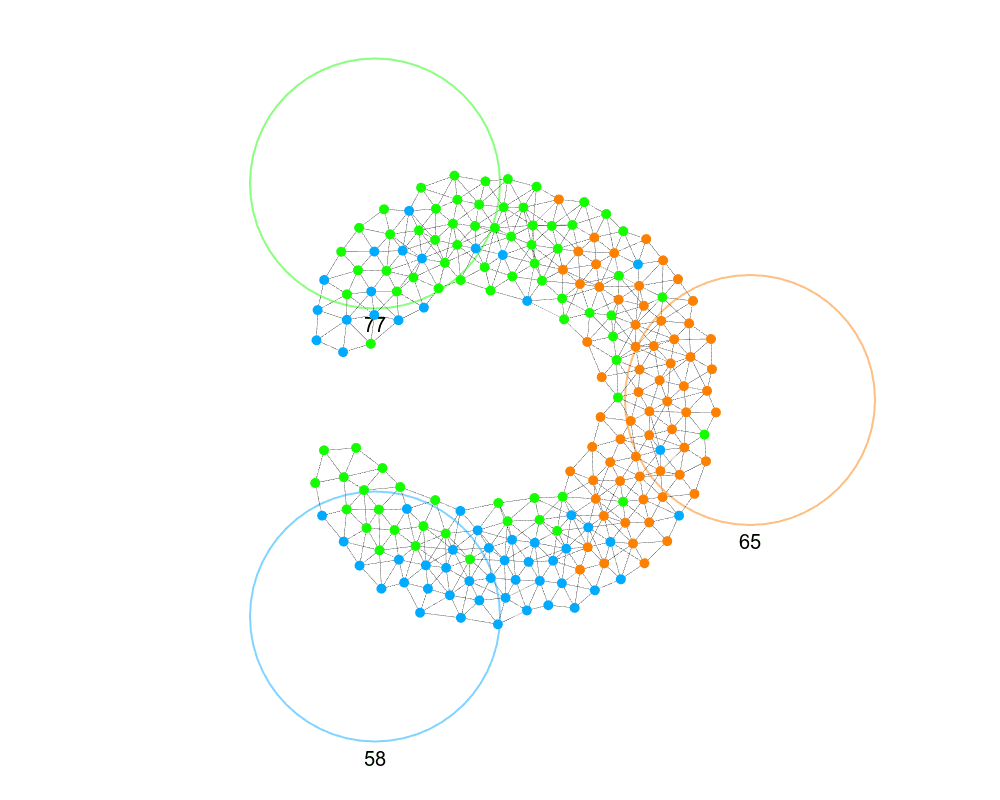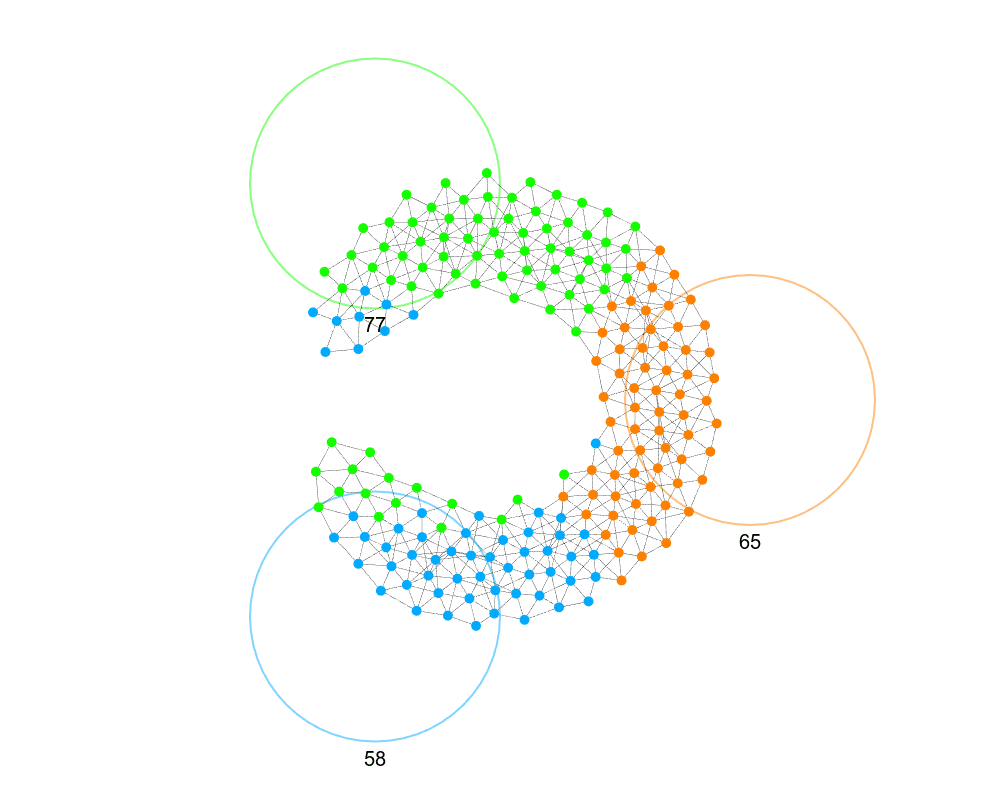
If a leader node flood-fills the network with a message containing groups and their positions, then each node can just randomly pick a group and move to its position (the colored circle).
This is highly robust, can be extended to handle weighted group assignment (e.g., 75% to one group and 25% to another), and handles dynamic networks without issue, but it is limited. The biggest issues with this naive implementation is that the groups are not the same size (although as the swarm increases the distribution should become more even) and the position of the nodes is completely ignored. Let’s see what we can do about these issues.
Position awareness
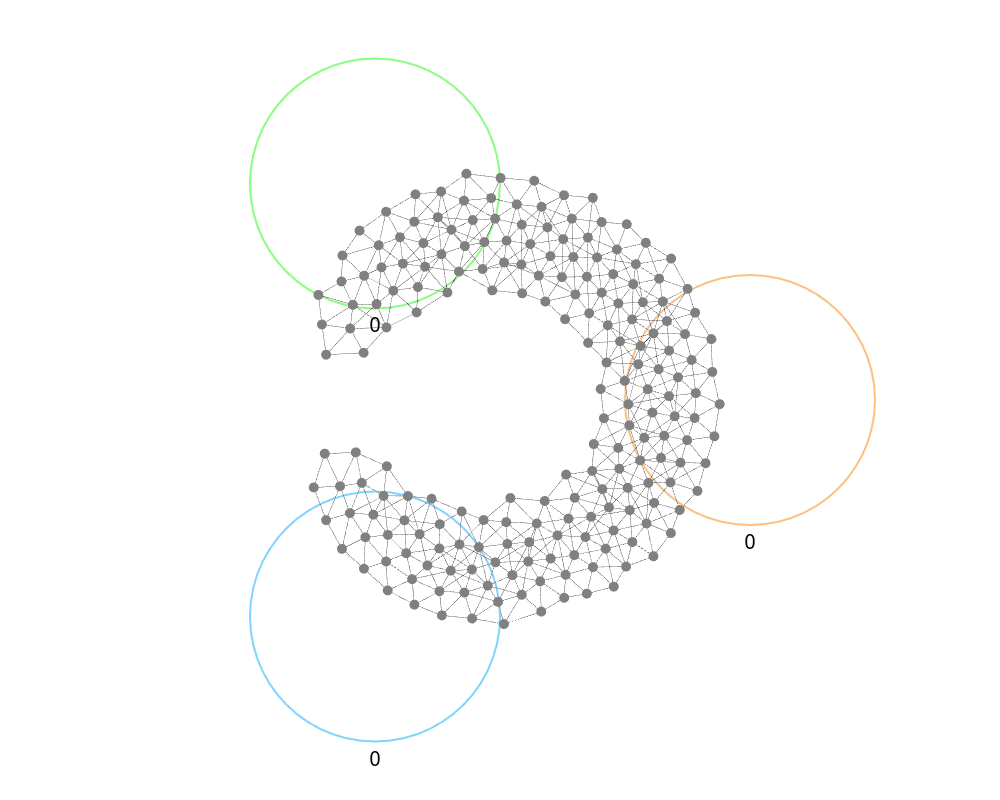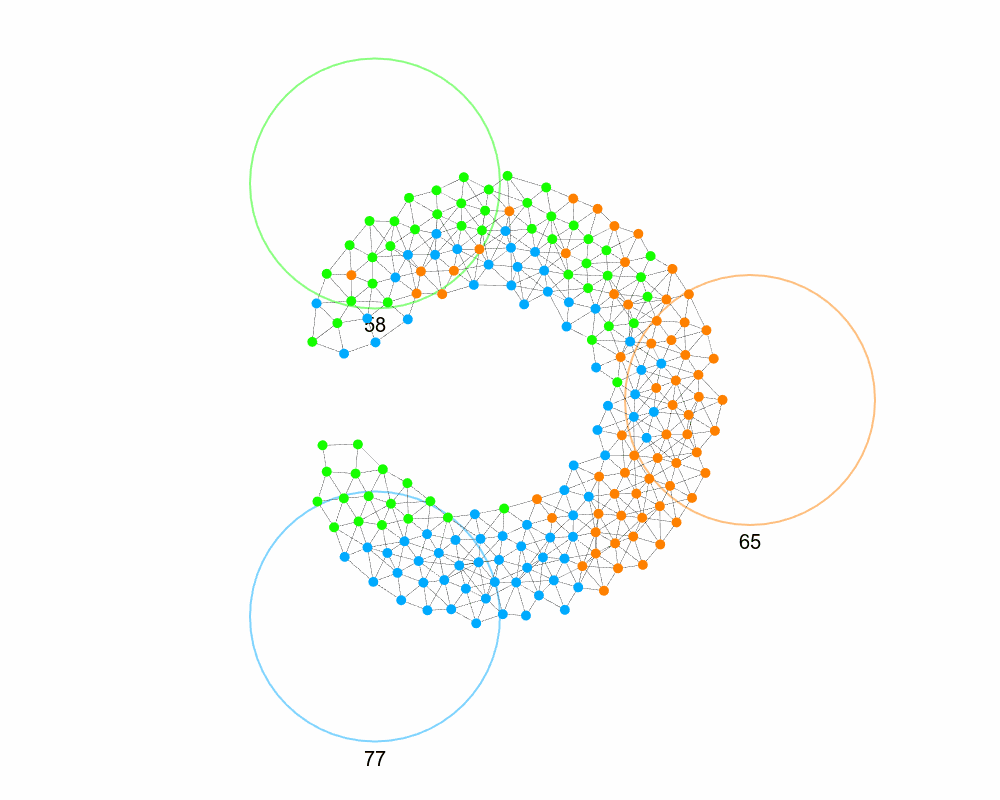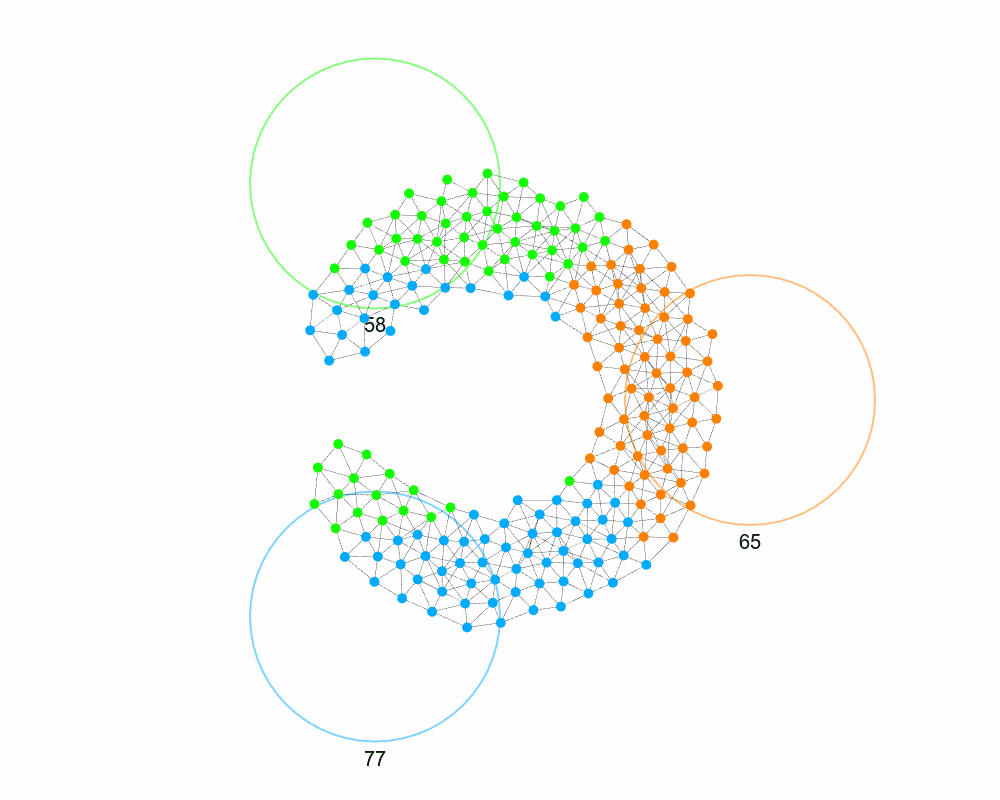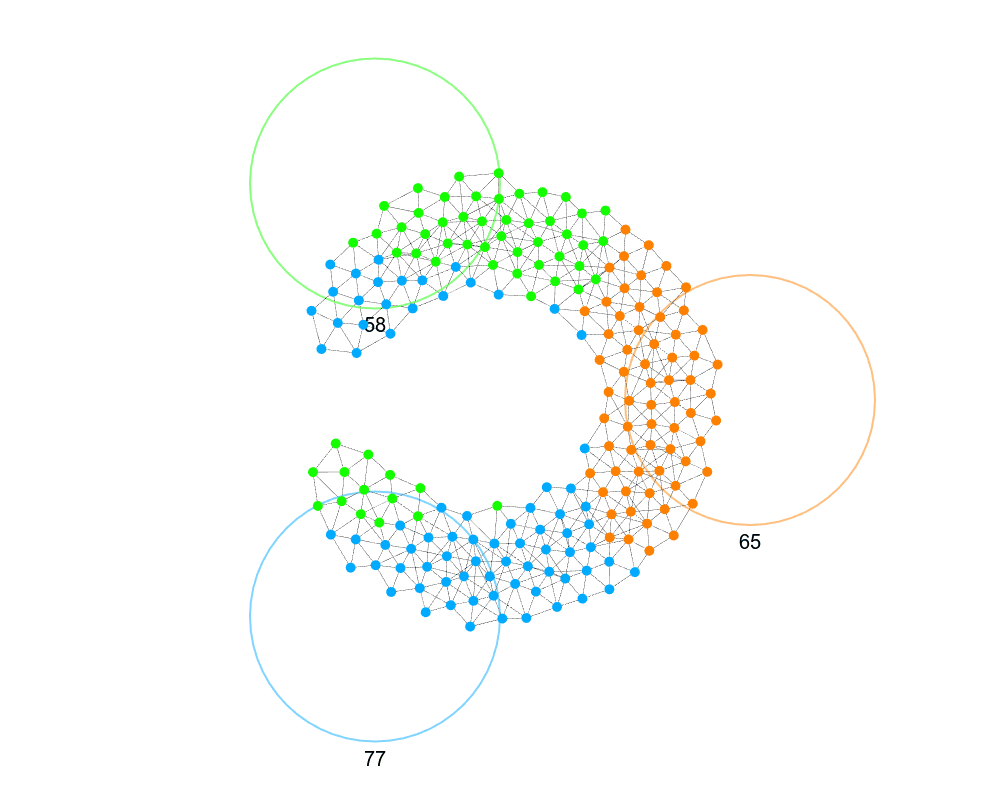
To make it position aware, what if after the group assignment we had nodes swap groups with their neighbors? In order to determine a good swap, a node can compare the sum of distances of itself and its neighbor to their destinations before and after a swap, and choose the one that minimizes the sum of the distances.
That is better, but two issues: the swarm doesn’t know when the swapping is finished (which is why they don’t move to the goals), and if we look at an example where the network is not convex, we realize this sorting can give suboptimal results. Here’s an example.
Swapping with neighbors to minimize distance can trap you in a local minimum: a node never swaps for a “worse” group, even if it would enable a better arrangement later. We see above how we see how some of the green and blue are unable to travel away from their target, even though temporarily doing so would allow them to get closer.
This problem is analogous to Simulated Annealing (SA), where you sometimes accept worse moves to escape local minima. Inspired by SA, instead of always selecting the best swap, a node samples from all possible swaps, weighting them by their improvement in distance. A temperature parameter is added to control how likely a node is to select a totally random node vs. the best swap. Early on, a higher temperature will balance the probabilities and encourages exploration; as the temperature decreases, the method becomes more greedy and will eventually only pick the best swap. The optimal initial temperature and cooling rate will vary depending on the network.
We have to speed up the swapping below since SA causes the sorting to take longer.
This is a tiny bit better, but in no way guarantees escaping local minima. This also requires picking parameters for the temperature, the cooling for the temperature, and when to stop. All this added complexity for a small benefit, it doesn’t seem worthwhile.
Going back to the simple sorting, we are still left with the issue of detecting when the swapping is complete.
Stopping signal
If we elect a leader, or in this case, elect the node that announced the initial partitioning, then that leader can monitor the swarm for when it has stopped swapping. The leader can send out heartbeat signals at a regular interval, which the nodes can use to keep track of how many hops they are from the leader, which in turn can be used to route information to the leader. The nodes will send back to the leader (through intermediate nodes) whether they are done swapping or not. This information can be reduced along the way to the leader with an $AND$, keeping the algorithm scalable. Once the leader sees that the swarm is finished swapping, it will flood-fill the network with a message letting the nodes they can move to their positions now.
This will work well, but it’s possible that the leader terminates prematurely. For example, if a small cluster of nodes is still swapping, but they suddenly move many hops away from the leader (imagine the swarm in a C shape, and the small cluster moves from one side of the gap in the C to the other side), then the signal will suddenly have a gap in it and the leader will falsely see for a few intervals that all the nodes are done swapping. This can be fixed by dynamically checking the radius of the swarm and ensuring the leader has heard from the farthest edges that the swapping has stopped.
We speed everything up since we are doing a lot now. The leader node is marked by a large circle, each node is colored according to its group, and each node is bolded if its subtree is finished swapping. We can see when a swap occurs and how this information propagates up the dynamic tree.
Unfortunately, this algorithm will fail in highly dynamic swarms. When the swapping is occurring faster then the network can reach the leader, then it will seem as if the swapping never terminates.
If you’re network is very fast relative to the robot movements then this isn’t a problem. Or, if we require the nodes to stop moving while we run the algorithm, then we would know that the group assignment will finish. That would be a far less general environment, but I think it’s one worth investigating.
Static network
If the nodes can’t move (at least not while the partitioning is occurring), then the swapping will terminate, and we can explore new algorithms and optimizations.
Let’s start by speeding up the signaling of swapping stopping. Instead of relying on a periodic heartbeat from the leader, nodes can directly notify their parent neighbors (those closer to the leader) once they finish swapping. This information propagates recursively until all nodes report completion.
This is a solution to the Distributed Termination Problem, a well-studied problem. It can be applied to any scenario where a network wants to detect when all of its nodes are completed with a task.
This is some good progress! But what about the unequal group sizes?
Trees
Once we build a tree from the leader, we can do a lot of neat things (assuming still that the nodes can’t move while the algorithm is running).
For instance, if each node counts how big its sub-tree is, then the leader can assign groups of exact sizes to every subtree. There are a few steps involved with that:
- The leader sends out a flood-fill that builds a tree (in this instance we have each node message the node it heard the broadcast from that it is the parent).
- When a node does not have any children (which it can track by listening for its neighbors and ensuring they all have parents), it marks itself as
countedand sends to its parent the value $1$. - When all of a nodes children are
counted, it will add up all their values to calculate its sub-tree size, then also mark itself ascountedand send the value to its parent. This is a recursive step, each node has its own sub-tree and is also a child of another sub-tree. - When the leader receives the final size of the entire swarm, it can determine how many nodes should be in each group (potentially weighted), and tell each sub-tree how many of its nodes are in each group.
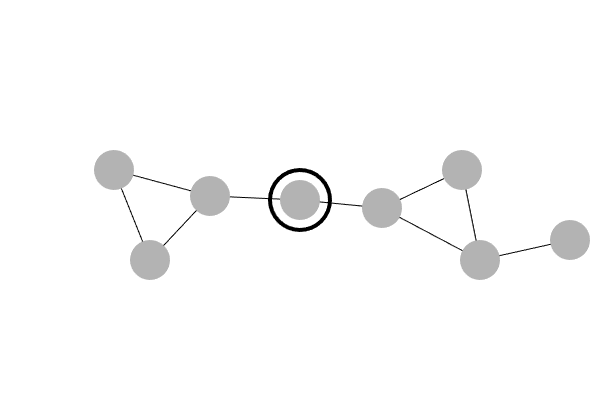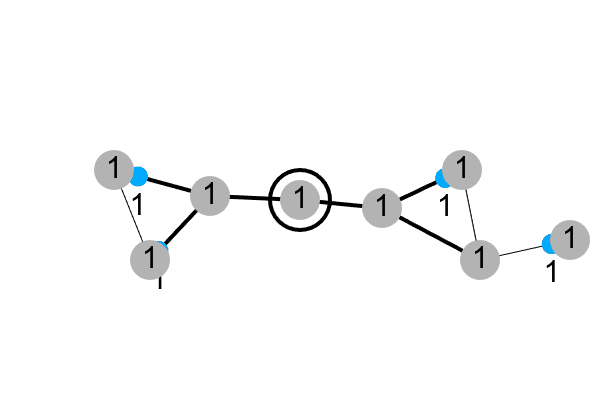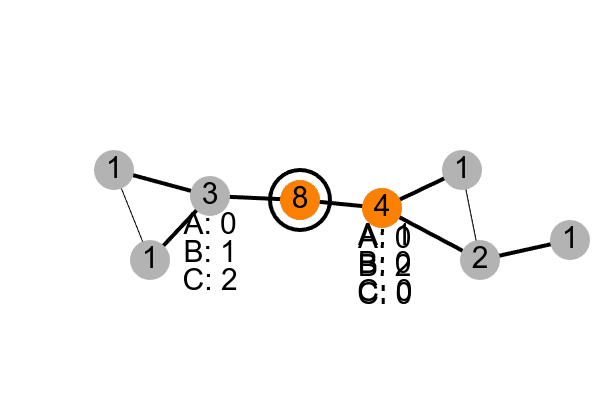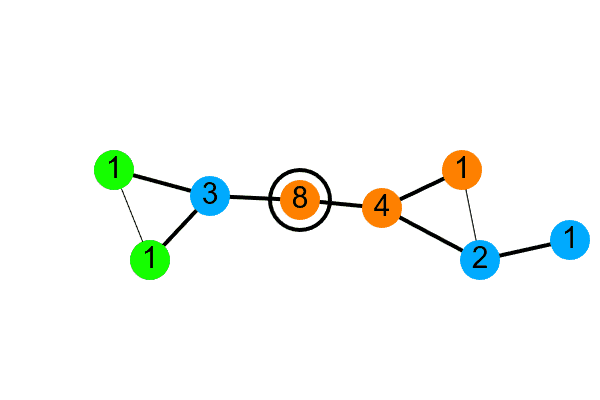
This is illustrated below. First, the tree is built (pink messages are INIT messages, and green messages let a node know that it is the parent), so nodes know who their parent and children are. Second, each leaf node sends its subtree size of $1$ to its parent (blue messages). Once a node has received all of the counts from its children, it sends its own subtree size up to its parent. Finally, the leader passes down the list of groups and how many nodes need to be assigned to each (red messages), with nodes assigning themselves to an available group before they pass it on.
In this example, the leader has two children, one with a subtree of size 3, and the other with a subtree of size 4. The leader then knows there are 8 nodes (3 + 4 + itself). We want 3 groups A, B, and C, so the leader decides there should be 3 nodes in A, 3 in B, and 2 in C. It assigns itself to A, tells its child with 4 nodes to assign 2 to A and 2 to B, and tells its child of 3 nodes to assign 1 to B and 2 to C. The children can run the same decision process, and the groups get assigned recursively.
And now we can run the same process on our larger network.
This gives us total control over the group size! So now we can pair that with the sorting to get a full algorithm for partitioning.
This is an partitioning that gives exact control over the group size and has some spatial awareness. It still has many issues, such as not supporting dynamic networks and not always providing an optimal assignment on non-convex networks, but it’s not too bad.
Variations
There are a couple of variations or improvements you might try on these static trees. The code for each animation is here, so you can can have a starting framework to implement these variations if you like.
Position-aware: You might be able to minimize the non-convex problem a bit if you add in position information to the tree assignment. If each node tracks the average position of its subtree, then groups can be assigned based on proximity to their target locations.
Groups of $K$: The leader can easily assign groups of $K$ rather then $K$ groups by simply choosing how many groups to have after calculating the swarm size. For example, if the leader finds it has 8 nodes and wants groups of 2, then it partitions into 4 groups.
Counting off nodes: The leader can also assign integer ranges to subtrees, and the nodes pick a single integer to assign itself. You could look at this as the leader deciding to have an equal number of groups as number of nodes (although that wouldn’t be as scalable, so we could use integer ranges). For example, if the leader find it has 8 nodes, then it assigns itself to ID $0$, assigns its child of 3 to the IDs $1-3$, and its other child of 4 to $4-7$.
You could actually use this counting-off protocol to assign groups. If you want $K$ groups, each node assigns itself to its ID modulo $K$. If you want groups of $K$, each node assigns itself to the floor of its ID divided by $K$. Note that this means if you can find a better way to count off nodes in the network, you also find a way to assign nodes to groups.
Other potential approaches
Instead of using these trees, there are other approaches we might explore in the future.
Density diffusion + token passing
There are two good papers that solve the problem of group assignment on a static graph using diffusion and token passing. This first paper solves the problem for two groups, and this second paper extends it to $K$ groups.
Pairing off
It would be worth investigating the problem of pairing off groups in a network, similar to how I imagine humans would solve this problem. If you asked a large group of people in an auditorium to get into groups of 100, how would they do it? One guess is that they would create small groups (maybe initially 2), each with a leader that tracks how big the group is, then the leaders would find each other and combine groups if the new group will be closer to the final answer, and repeat. You would still need to handle groups that would get too big, leadership election, group merges, and other issues.
Distributed K-means clustering
Using the Distributed K-means Clustering Algorithm allows you to assign position-aware group assignments, but only for static networks. Unfortunately, this doesn’t solve the problem of equal-sized groups. Perhaps the centralized same-size K means clustering algorithm could be extended to the distributed setting? It certainly seems possible. Could that be extended to the dynamic setting?