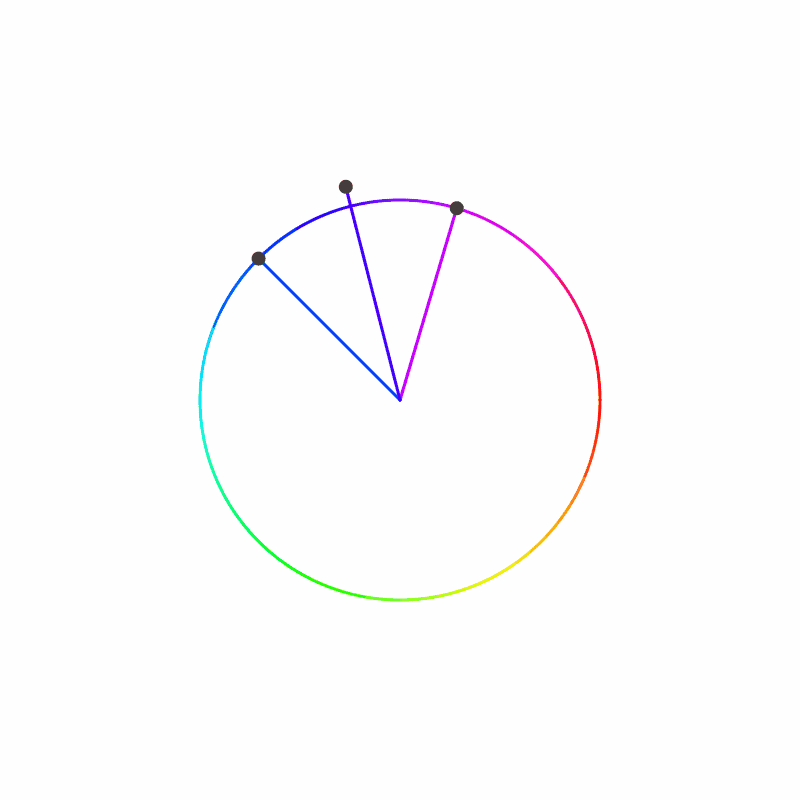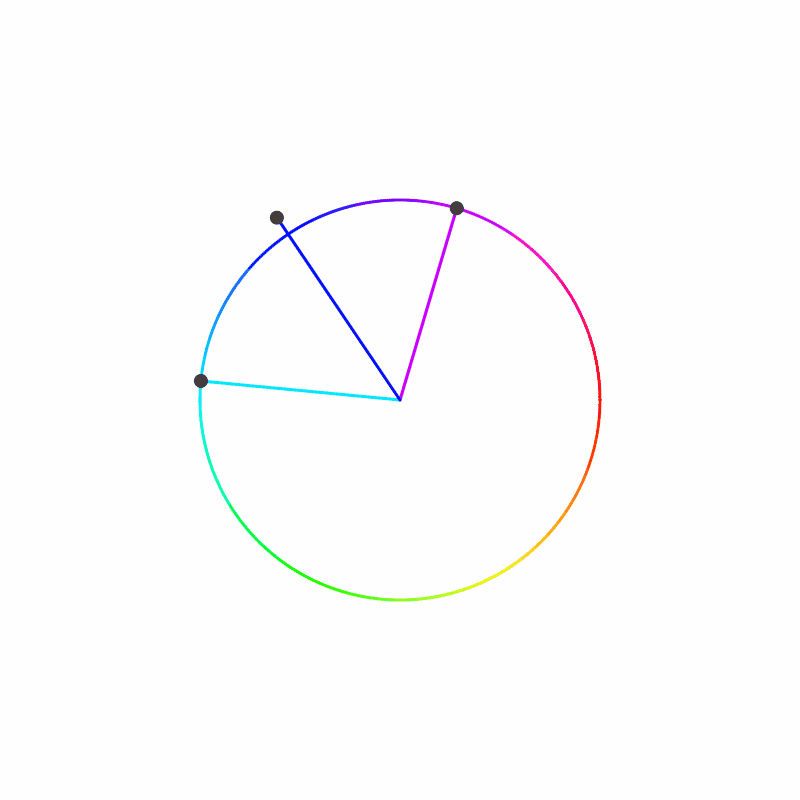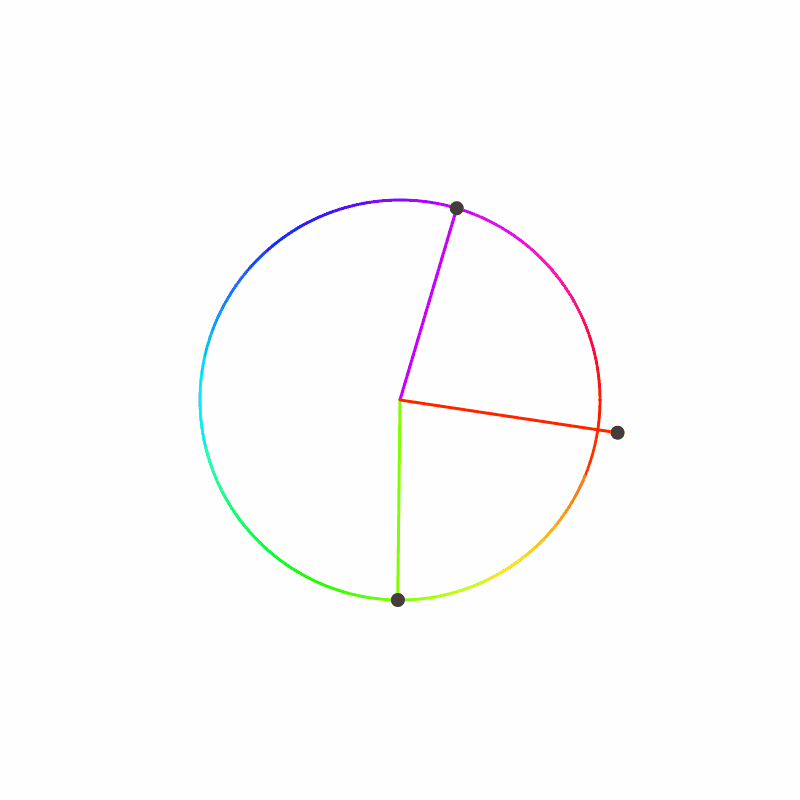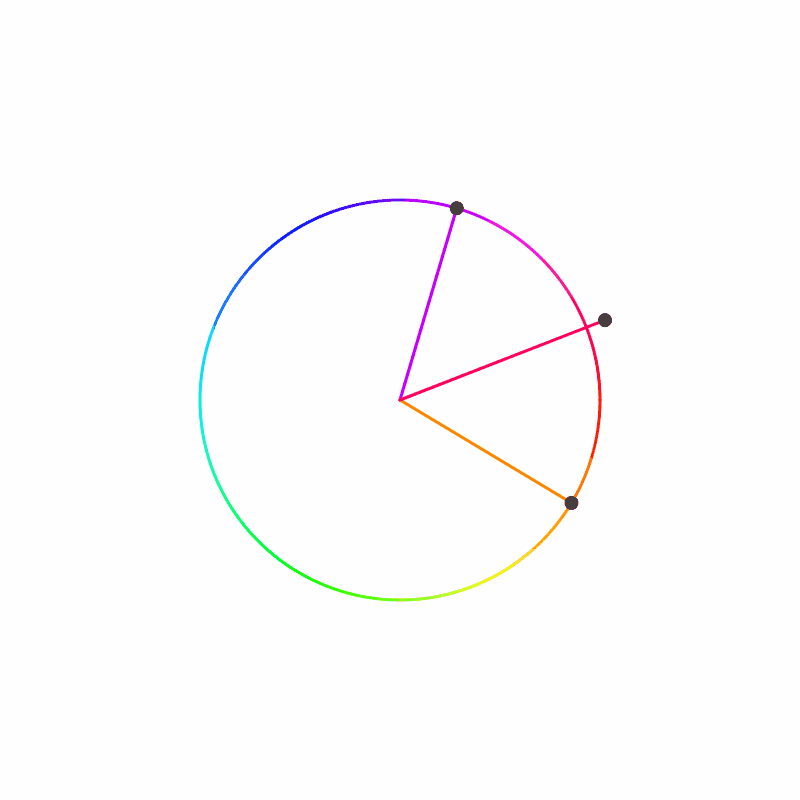I came across an interesting problem in a previous post where boids would get stuck while trying to “vote” on the rotation of a shape. Let’s explore different voting mechanisms in a swarm and see what happens.
Voting Strategies
First let’s look at a simple case: voting on a scalar. Everyone starts with a random number, and then they receive their neighbor’s values every second or so. There are multiple strategies we could choose for what a boid does when receiving a value:
- Highest value: If the incoming value is higher than our current value, then replace our current with that value. This strategy will lead to the group eventually agreeing on the largest value in the swarm.
- Random: Some percent of the time you replace your current value with the incoming value. There is no guarantee the swarm will eventually agree on a value.
- Average: Replace your current value with the average of the incoming value and your current value. This will cause the swarm to eventually all agree on what is essentially the average of all the swarm’s initial values.
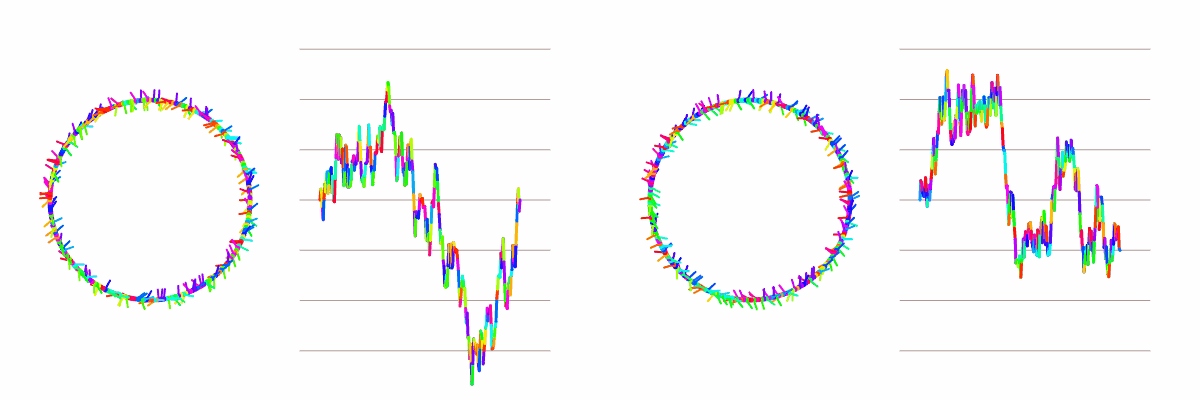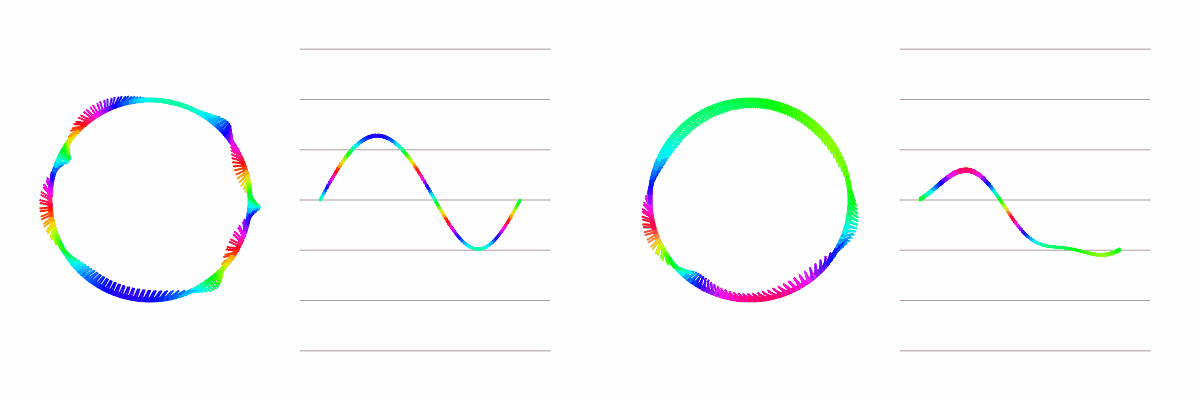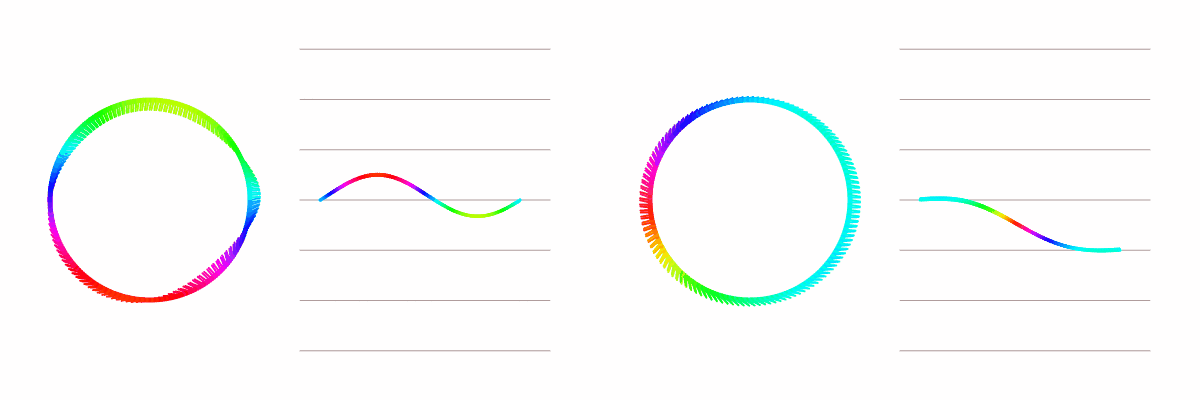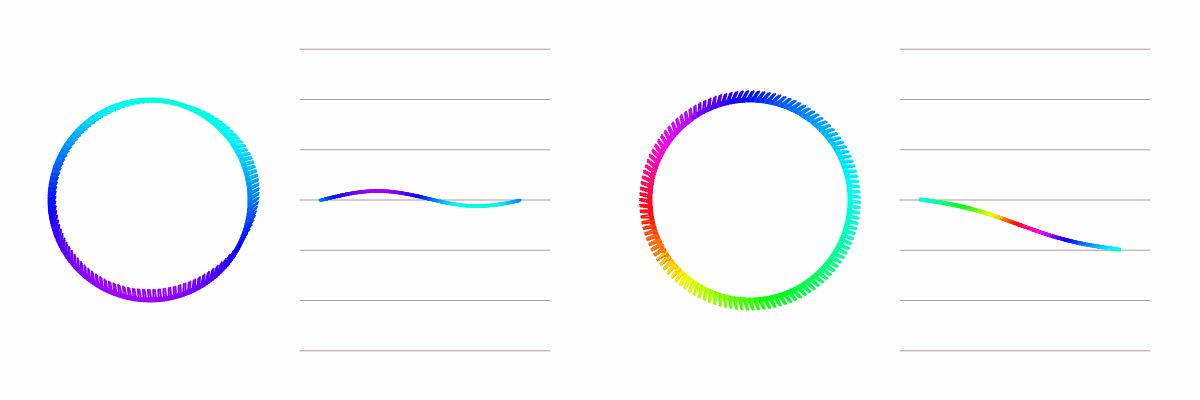
For a simplified environment, let’s look at a grid of squares. The squares initialize with random values and will be colored based on their value (grayscale with black as 0 and white as 1). Each square will look at its neighboring squares and use one of the above methods to modify its value. From left to right we see the strategies of Highest, Random, and Average.
We see that only Highest and Average result in all squares reaching agreement, but note that with Average, the values are not exactly the same.
If we consider voting on a vector of scalars we see all the strategies still apply (you could even use different strategies for each dimension).
For labels (like “Apple” and “Orange”) you could only use Random. However, if you create some ordering on the values (so length wouldn’t work since different labels could have the same length, but converting the letters to numbers of a 26-base number system would), then you could use Highest.
For rotations (values on a unit circle) we could use all three strategies, but averaging looks a bit different. Random works for all types of values, Highest can be used by considering the angle as an input, but for Averaging we need a new strategy. The average of 20 degrees and 60 degrees seems simple enough, it should be 40 degrees. But what about the average of 20 degrees and 300 degrees? The correct answer should be 340, not 160. Below we see what averaging on a circle might look like.
Note that this concept of “averaging” fails when the two values are exactly 180 degrees from each other, which is an edge case we will ignore.
Let’s use this new concept of averaging on the grid of squares, which will now store a rotational value rather than a scalar. Below are the squares running the Average strategy, represented with squares and also with arrows so we can get a more clear idea of what’s going on.
We note some interesting behavior here, specifically that there are these unstable regions where all angles are being voted for, but they don’t always disappear, sometimes they wander. If you look closely you can find three different types: all pointing in or out around a point, all rotating around a point, or a saddle point. Keep this in mind for later.
But let’s relate this back to the boids issue that started this all off. Rather than a grid of boids, we were looking at a circle of boids (it was actually an annulus). So let’s run the same simulation as above, but instead of squares on a grid, we use agents on a circle.
On a circle
And we see the issue that began this investigation, the agents do not all converge to the same value. Given initially random values, they seem to settle on cycles of the value, the number of cycles different each time. Could we predict what the final result will look like given the initial configuration? Yes!
Let us start at a point on the circle, then add up the change in angle as we travel around the circle (including the angle between the last and first agent). Let’s graph that sum with the x-axis being the angle traveled. We will also draw a vertical line for every 360 degrees on the graph. We know the sum must land on one of these vertical lines (think through with 3 agents to get an intuition of why).
We have on the left a swarm that converges to a single value, and to the right a swarm that converges to one cycle of values. We notice that the swarm that converges to a single value had the sum land on the same vertical line that it started on, while the swarm with a cycle of values had the sum land one vertical line away.
This technique allows us to determine the end result for any initial beliefs and whether they will disagree or not, more than that, how many times they will cycle the disagreement and in what direction.
There is a continuous analog of this problem. If you define a complex function from the agents in their circle (or square, whatever shape they are outlining) to values on the unit circle, then you can consider the function as a curve and find its winding number around 0. Intuitively you can see this below. The agents are in the shape of a diamond outline, and as you travel along that outline you get complex values, which define a curve. The winding number is the mathematical equivalent of counting the number of times a curve travels around a point, and since our curve travels along the unit circle, we can use 0 as our point.
We see the winding number is positive two for this function on the diamond. This tells us the swarm (in the continuous sense) will settle with values cycling twice around the diamond in the clockwise direction.
How might similar issues arise in other shapes and different dimensions? In order to better explore those places it is easier to work in the purely mathematical world.
Continuous function representation (under construction)
One approximation is to define “valid” configurations to be all the continuous functions from the surface to the unit circle. Already we know this is an approximation since in the case where the surface was a square we saw disagreement points (sinks, sources, rotations, saddles), which are not continuous at those points. But let us ignore these discrepancies and play in this new space.
What we do is imagine all the possible continuous functions from the surface to the unit circle, then imagine the limit as those functions change according to the averaging strategy (what does it look like in continuous space?), and then consider if there exist any limits which are not just the constant function.
Let’s take the diamond outline we’ve seen above. There are many functions, which in their limits are the constant function, anything which has a winding value of 0. But then there are also functions whose limit is not a constant function, namely those with winding values non-zero.
On the square, I can’t imagine any function whose limit is not the constant function. Similarly, for the sphere can I imagine no such function. This may remind us of the Hairy Ball Theorem, but it is not quite the same, a quick counter-example shows us why. The constant function on the sphere is perfectly fine in our situation, but not for the Hairy Ball Theorem. Our values have no need to be tangent to the surface, their only constraint is to be continuous on the surface.
Could there be a non-constant limit function on the sphere? I don’t believe so. A property of the averaging function I believe would exist is that the winding value on any closed curve over the surface would stay constant. This means we don’t actually need to consider the limit of the averaging function, we simply need to look at all the possible closed curves and their winding values. Another property I suspect is true is that the winding value of a closed curve does not change as you smoothly deform it. If all these properties hold, then we could conclude a sphere must always have the constant value as its function. If it did not, then there exists some closed curve with a non-zero winding value, but that curve can be smoothly deformed into an arbitrarily small circle, which on a continuous surface must eventually result in a winding value of zero.
But if we did need to define smoothing a continuous function from a surface to the unit circle, what might it look like?
- Vector fields: Can we consider the rotations as vectors, and then hope to smooth out a vector field? Could we take each component of the vectors and apply the heat equation to them? This may result in vectors not on the unit circle, which we would need to fix.
- Locally scalars: If you zoom in close enough, then the surface should look like it maps to scalars by replacing the rotations with their angles. Some offset might be needed so jumps from 0 to 360 don’t exist, which we know we can do since the function is continuous, so we can zoom in close enough that all the considered angles are within 360 degrees of each other. Then the heat equation again.