Universal Codes for Variable-length Encoding

It is very common in networking to use a fixed-size header in front of a packet to tell us how big the rest of the packet is. This allows for dynamically sized packets but imposes a limit on the maximum packet size it can support. How can we support arbitrarily large packet sizes?

One standard is Variable Byte Encoding (Varint), where continuation bits are used at the end (or start) of every byte.

For example, we might have a payload of 14 bits (the gray xs below). We insert a continuation bit (red) every 8th bit, with a 0 indicating the message continues, and a 1 indicating the message is terminated.

You decode this by reading 8 bits at a time. If the last bit is 1, the message terminates; otherwise, continue reading. But we can’t always recover the original payload since padding can make it ambiguous how long the original payload was (such as if our payload was 20 bits). We can instead use a continuation bit every other bit instead of every 8th bit, then no padding is needed. It just looks like alternating between payload and continuation bits.

Let’s call the first encoding scheme VarInt-8, and the second VarInt-2.

If the input payload has $N$ bits, then VarInt-2 will use $2N$ bits, which means there are $N$ overhead bits (the bits other than the payload). This is quite inefficient, and there must be a more efficient encoding scheme that results in fewer overhead bits.

Instead of inter-weaved continuation bits, we can use a header at the beginning of our message, indicating how long the following payload is. If the payload has 20 bits, then the header should encode 20 (10100 in binary). The header is variable length as well, so for now, we will use VarInt-2 to encode it.

The header bits indicating the size will be colored green, and the continuation bits will still be red.

You decode this by reading the header until it terminates, then use that decoded value to determine how many following bits to read as the payload. This is much more efficient since the encoding of a payload of $N$ bits now uses $2 (\lfloor \log_2 N \rfloor + 1)$ overhead bits. A logarithmic overhead scales better than a linear overhead. But we can do even better.

Instead of using continuation bits in the header, why not pretend the header is itself a payload and just use another header? We can repeat this until the smallest header uses 2 bits (not 1 bit since that would only allow a header to at most indicate the next header has 1 bit). As an example, if the payload has length 20, then the first header will be 10100. Then 10100 has length 5, so the second header is 101, which has length 3, so the final header is 11. We concat these headers in the order of smallest to largest since we know we start with 2 bits, then we read how big the next header is, and so on. We can tell when we reach the final payload by using a continuation bit at the end of each header. In our example, that makes the full combined header below.

To decode this, you always start by reading the first two bits to determine the size of the next part of the packet, then if the continuation bit is 1 you will know that the following read is the last, otherwise repeat. For a payload size of 20 this encoding has more bits compared to the single header, but as we scale, this encoding will be more efficient. But we can improve it even more.

Notice that every sub-header (the individual headers making up the combined header) must start with a 1, which makes sense since otherwise we would have an unnecessary leading 0, and we would shorten the previous header. This means we can assume every header starts with a 1 and remove it from the encoding.

Again, if the payload has length 20, the first header will be 10100, but if we ignore the leading 1, it’s 0100. The first header now has length 4, so the second header is 100 and without the leading 1 it’s 00. Similarly, the final header is 0. We can create the final encoding as we did above, using the headers with continuation bits.

We decode this the same way we decoded the previous encoding, but we add back in the leading 1 to each header.

This scheme results in overhead approximately proportional to repeated logarithms of $N$, specifically: $ \lfloor \log_2 N \rfloor + \lfloor \log_2 \lfloor \log_2 N \rfloor \rfloor + …$ This is significantly smaller than a linear or even a single logarithmic overhead. But can we do better?

Doing some research, it turns out what we are building is called Universal Codes, which have some provably optimal solutions (at least asymptotically). One such example is Elias omega coding, which looks very similar to our encoding scheme. In fact, our solution is Elias omega coding, except we remove the leading 1 since it can be implied. There are many other available encoding schemes, each of which follows a different probability distribution for message lengths.

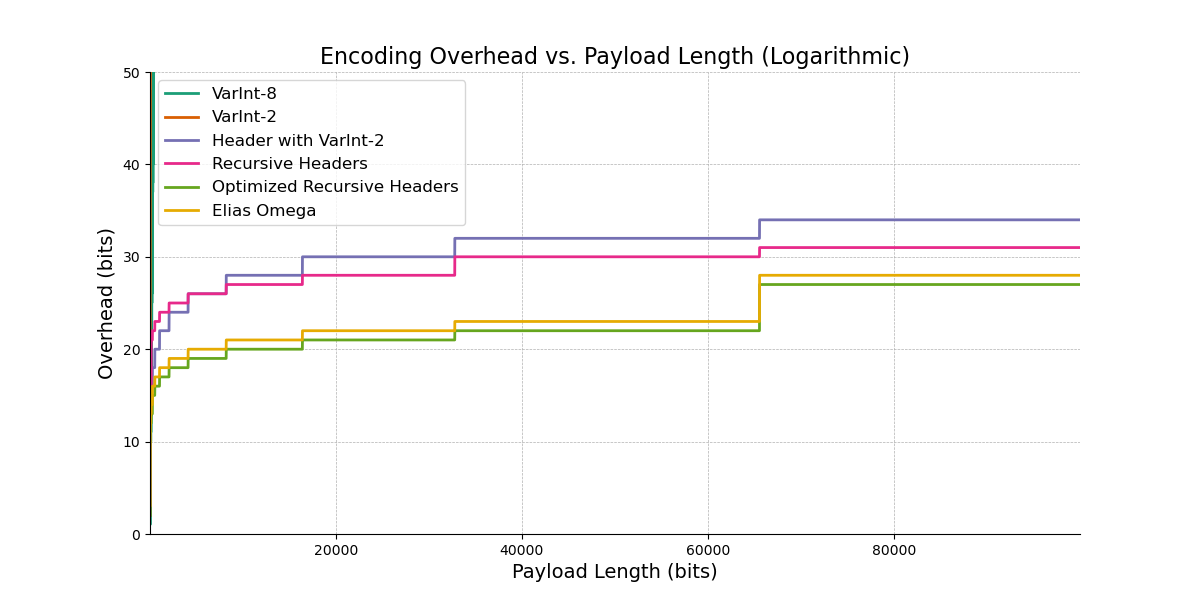
We can compare the overhead of all our encoding schemes (and Elias omega) for a number of payload sizes, which we plot below. Code is also provided to encode, decode, and plot all these schemes.

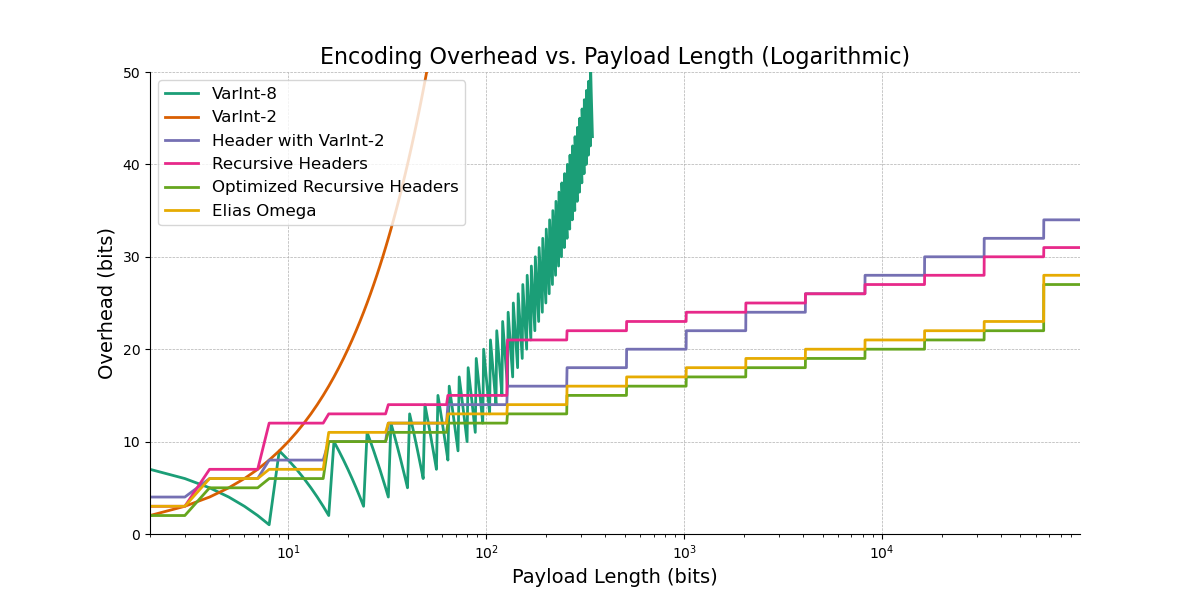
First we see the plot of overhead bits for each encoding scheme, but its a bit hard to read (VarInt goes off the screen), so let’s also look at the plot using a log scale x-axis.

We can see how each iteration shrinks the overhead bits, even eventually shaving a bit off of a standard Universal code. This is useful if we ever want to implement a variable length encoding for arbitrary large payloads.

A future exploration could be to analyze optimal encoding schemes when the probability distribution of message sizes is known. For example, if most messages are between 1GB and 2GB, but others are rare, how should the header be structured to minimize overhead?

Code for encoding and decoding.

def binary_string(n: int) -> str:
    """Convert an integer to its binary string representation without the '0b' prefix."""
    return bin(n)[2:]


#########################################
# Scheme 1: Continuation Bits Every k Bits
#########################################


def encode_continuation_bits(payload: str, k: int) -> str:
    """Encodes a binary payload by inserting continuation bits every k bits."""
    # Pad the payload to be a multiple of k bits
 payload = "0" * ((k - (len(payload) % k)) % k) + payload

 encoded = []
    for i in range(0, len(payload), k):
 encoded.append(payload[i : i + k])
 encoded.append("1")  # Add continuation bit

 encoded[-1] = "0"  # Last continuation bit becomes a termination bit
    return "".join(encoded)


def decode_continuation_bits(encoded: str, k: int) -> str:
    """Decodes a binary string encoded with continuation bits every k bits."""
 pos = 0
 decoded_bits = []

    while pos + k <= len(encoded):
 decoded_bits.append(encoded[pos : pos + k])
 pos += k

        if encoded[pos] == "0":  # Termination marker
            break
 pos += 1  # Skip the continuation marker

    return "".join(decoded_bits)


#########################################
# Scheme 2: Single Header with Interleaved Continuation Bits
#########################################


def encode_single_header(payload: str) -> str:
    """Encodes a binary payload with a single interleaved header."""
 header = "".join(bit + "0" for bit in binary_string(len(payload)))[:-1] + "1"
    return header + payload


def decode_single_header(encoded: str) -> str:
    """Decodes a binary string encoded with a single interleaved header."""
 pos = 0
 header_bits = ""

    while pos < len(encoded) - 1:
 header_bits += encoded[pos]
 pos += 2  # Skip continuation bits
        if encoded[pos - 1] == "1":  # End of header
            break

 payload_length = int(header_bits, 2)
    return encoded[pos : pos + payload_length]


#########################################
# Scheme 3: Multi-Level Header (Non-Optimized)
#########################################


def encode_multi_level_header(payload: str) -> str:
    """Encodes a binary payload using a multi-level header."""
 headers = []
 current = len(payload)

    while True:
 header = binary_string(current)
 headers.append(header)
        if len(header) == 2:
            break
 current = len(header)

 encoded_header = "".join(header + "0" for header in reversed(headers))[:-1] + "1"
    return encoded_header + payload


def decode_multi_level_header(encoded: str) -> str:
    """Decodes a binary string encoded with a multi-level header."""
 pos, header_length = 0, 2

    while True:
 header = encoded[pos : pos + header_length]
 pos += header_length

        if encoded[pos] == "1":
            break

 pos += 1  # Skip continuation bit
 header_length = int(header, 2)

    return encoded[pos + 1 : pos + 1 + int(header, 2)]


#########################################
# Scheme 4: Optimized Multi-Level Header (Drop Leading '1')
#########################################


def encode_optimized_multi_level_header(payload: str) -> str:
    """Encodes a binary payload using an optimized multi-level header that drops the leading '1'."""
 headers = []
 current = len(payload)

    while True:
 header = binary_string(current)[1:]
 headers.append(header)
        if len(header) == 1:
            break
 current = len(header)

 encoded_header = "".join(header + "0" for header in reversed(headers))[:-1] + "1"
    return encoded_header + payload


def decode_optimized_multi_level_header(encoded: str) -> str:
    """Decodes a binary string encoded with an optimized multi-level header."""
 pos, header_length = 0, 1

    while True:
 header = encoded[pos : pos + header_length]
 pos += header_length

        if encoded[pos] == "1":
            break

 pos += 1  # Skip continuation bit
 header_length = int("1" + header, 2)

    return encoded[pos + 1 : pos + 1 + int("1" + header, 2)]


#########################################
# Scheme 5: Elias Omega Coding
#########################################


def encode_elias_omega(payload: str) -> str:
    """Encodes a binary payload using Elias Omega coding."""
 N = len(payload)
 code = "0"

    while N > 1:
 code = binary_string(N) + code
 N = len(binary_string(N)) - 1

    return code + payload


def decode_elias_omega(encoded: str) -> str:
    """Decodes a binary string encoded with Elias Omega coding."""
 pos, N = 0, 1

    while encoded[pos] == "1":
 read_range = N + 1
        if pos + read_range > len(encoded):
            raise ValueError("Malformed encoding: unexpected end before payload.")
 N = int(encoded[pos : pos + read_range], 2)
 pos += read_range

    return encoded[pos + 1 : pos + 1 + N]


#########################################
# Examples
#########################################

if __name__ == "__main__":
 test_payloads = [
        "10001",
        "101010",
        "1100110011",
        "111000111000111",
        "0" * 20,
        "1" * 37,
 ]
 schemes = [
 (
            "Scheme 1 (k=7)",
            lambda p: encode_continuation_bits(p, 4),
            lambda p: decode_continuation_bits(p, 4),
 ),
 (
            "Scheme 1 (k=1)",
            lambda p: encode_continuation_bits(p, 1),
            lambda p: decode_continuation_bits(p, 1),
 ),
 ("Scheme 2 (Single Header)", encode_single_header, decode_single_header),
 (
            "Scheme 3 (Multi-Level Header)",
 encode_multi_level_header,
 decode_multi_level_header,
 ),
 (
            "Scheme 4 (Optimized Multi-Level Header)",
 encode_optimized_multi_level_header,
 decode_optimized_multi_level_header,
 ),
 ("Scheme 5 (Elias Omega)", encode_elias_omega, decode_elias_omega),
 ]

    for name, encode_fn, decode_fn in schemes:
        print(f"--- Testing {name} ---")
        for payload in test_payloads:
 encoded = encode_fn(payload)
 decoded = decode_fn(encoded)

            print(f"\tPayload:\t{payload}")
            print(f"\tEncoded:\t{encoded}")
            print(f"\tDecoded:\t{decoded}")

            print(
                f"payload len={len(payload):3d} encoded len={len(encoded):3d} overhead={len(encoded)-len(payload):3d}"
 )
        print()

Code for plotting the overhead.

import matplotlib.pyplot as plt
from schemes import *

# Define a larger payload range for better resolution
payload_lengths = list(range(2, 100000))

# Define the encoding schemes
schemes = [
 ("VarInt-8", lambda p: encode_continuation_bits(p, 8)),
 ("VarInt-2", lambda p: encode_continuation_bits(p, 1)),
 ("Header with 2-VarInt", encode_single_header),
 ("Recursive Headers", encode_multi_level_header),
 ("Optimized Recursive Headers", encode_optimized_multi_level_header),
 ("Elias Omega", encode_elias_omega),
]

# Define a threshold for maximum overhead
max_overhead = 50

# Compute overhead for each scheme, stopping when overhead exceeds the threshold
overhead_data = {}
valid_payload_lengths = {}

for name, encode_fn in schemes:
 overhead_values = []
 payload_lengths_filtered = []

    for length in payload_lengths:
 payload = "1" * length  # Use a simple payload of all 1s
 encoded = encode_fn(payload)
 overhead = len(encoded) - length

        if overhead > max_overhead:
            break  # Stop collecting data once overhead exceeds the threshold

 overhead_values.append(overhead)
 payload_lengths_filtered.append(length)

 overhead_data[name] = overhead_values
 valid_payload_lengths[name] = payload_lengths_filtered

# Create the plot
plt.figure(figsize=(12, 7))

# Use distinct line styles and make them more visible
colors = plt.get_cmap("Dark2").colors  # Deep, slightly muted colors
max_x = max(max(lengths) for lengths in valid_payload_lengths.values())

for i, (name, overhead) in enumerate(overhead_data.items()):
 plt.plot(
 valid_payload_lengths[name],
 overhead,
        label=name,
        color=colors[i % len(colors)],
        linewidth=2,
 )

# Improve plot aesthetics
plt.xlabel("Payload Length (bits)", fontsize=14)
plt.ylabel("Overhead (bits)", fontsize=14)
plt.title(
    f"Encoding Overhead vs. Payload Length",
    fontsize=16,
)
plt.legend(fontsize=12, loc="upper left")
plt.grid(True, linestyle="--", linewidth=0.5)
# plt.xscale("log")  # Use logarithmic scale for better visualization of trends
plt.ylim(0, max_overhead)  # Adjust y-limit slightly above max_overhead
plt.xlim(2, max_x)  # Set x-limit to the max valid payload length

# Remove top and right border lines
ax = plt.gca()
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)

plt.show()