People say many things about entropy: entropy increases with time, entropy is disorder, entropy increases with energy, entropy determines the arrow of time, etc.. But I have no idea what entropy is, and from what I find, neither do most other people. This is the introduction I wish I had when first told about entropy, so hopefully you find it helpful. My goal is that by the end of this long post we will have a rigorous and intuitive understanding of those statements, and in particular, why the universe looks different when moving forward through time versus when traveling backward through time.
This journey begins with defining and understanding entropy. There are multiple formal definitions of entropy across disciplines—thermodynamics, statistical mechanics, information theory—but they all share a central idea: entropy quantifies uncertainty. The easiest introduction to entropy is through Information Theory, which will lead to entropy in physical systems, and then finally to the relationship between entropy and time.
Information Theory
Imagine you want to communicate to your friend the outcome of some random events, like the outcome of a dice roll or the winner of a lottery, but you want to do it with the fewest number of bits (only 1s and 0s) as possible. How few bits could you use?
The creator of Information Theory, Claude Shannon, was trying to answer questions such as these during his time at Bell labs. He was developing the mathematical foundations of communication and compression, and eventually he discovered that the minimum number of bits required for a message was directly related to the uncertainty of the message. He was able to then formulate an equation to quantify the uncertainty of a message. When he shared it with his physicist colleague at Bell Labs, John von Neumann, von Neumann suggested calling it entropy for two reasons:
Von Neumann, Shannon reports, suggested that there were two good reasons for calling the function “entropy”. “It is already in use under that name,” he is reported to have said, “and besides, it will give you a great edge in debates because nobody really knows what entropy is anyway.” Shannon called the function “entropy” and used it as a measure of “uncertainty,” interchanging the two words in his writings without discrimination.
— Harold A. Johnson (ed.), Heat Transfer, Thermodynamics and Education: Boelter Anniversary Volume (New York: McGraw-Hill, 1964), p. 354.
Later we will see that the relationship between Shannon’s entropy and the pre-existing definition of entropy was more than coincidental, they are deeply intertwined.
But now let us see how Shannon found definitions for these usually vague terms of “information” and “uncertainty”.
In Information Theory, the information of an observed state is formally defined as the number of bits needed to communicate that state (at least for a system with equally likely outcomes with powers of two, we’ll see shortly how to generalize this). Here are some examples of information:
- If I flip a fair coin, it will take one bit of information to tell you the outcome: I use a
0for head and a1for tails. - If I roll a fair 8-sided dice, I can represent the outcome with 3 bits: I use
000for a 1,001for 2,010for 3, etc.
The more outcomes a system can have, the more bits (information) it will require to represent its outcome. If a system has $N$ equally likely outcomes, then it will take $\text{log}_2(N)$ bits of information to represent an outcome of that system.
Entropy is defined as the expected number of bits of information needed to represent the state of a system (this is a lie, but it’s the most useful definition for the moment, we’ll fix it later). So the entropy of a coin is 1 since on average we expect it to take 1 bit of information to represent the outcome of the coin. An 8-sided dice will have an entropy of 3 bits, since we expect it to take an average of 3 bits to represent the outcome.
It initially seems that entropy is an unnecessary definition since we can just look at how many bits it takes to represent the outcome of our system and use that value, but this is only true when the chance of the outcomes are all equally likely.
Imagine now that I have a weighted 8-sided dice, so the number 7 comes up $50$% of the time while the rest of the faces come up $\approx 7.14$% of the time. Now, if we are clever, we can reduce the expected number of bits needed to communicate the outcome of the dice. We can decide to represent a 7 with a 0, and all the other numbers will be represented with 1XXX where the Xs are some unique bits. This would mean that $50$% percent of the time we only have to use 1 bit of information to represent the outcome, and the other $50$% of the time we use 4 bits, so the expected number of bits (the entropy of the dice) is 2.5. This is lower than the 3 bits of entropy for the fair 8-sided dice.
Fortunately, we don’t need to come up with a clever encoding scheme for every possible system, there exists a pattern to how many bits of information it takes to represent a state with probability $p$. We know if $p=0.5$ such as in the case of a coin landing on heads, then it takes 1 bit of information to represent that outcome. If $p=0.125$ such as in the case of a fair 8-sided dice landing on the number 5, it takes 3 bits of information to represent that outcome. If $p=0.5$ such as in the case of our unfair 8-sided dice landing on the number 7, then it takes 1 bit of information, just like the coin, which shows us that all that matters is the probability of the outcome. With this, we can discover an equation for the number of bits of information needed for a state with probability $p$.
\[I(p) = -\text{log}_2(p)\]This value $I$ is usually called information content or surprise, since the lower the probability of a state occurring, the higher the surprise when it does occur.
When the probability is low, the surprise is high, and when the probability is high, the surprise is low. This is a more general formula then “the number of bits needed” since it allows for states that are exceptionally likely (such as $99$% likely) to have surprise less then 1, which would make less sense if we tried to interpret the value as “the number of needed bits to represent the outcome”.
And now we can fix our definition of entropy (the lie I told earlier). Entropy is not necessarily the expected number of bits used to represent a system (although it is when you use an optimal encoding scheme), but more generally the entropy is the expected surprise of the system.
And now we can calculate the entropy of systems like a dice or a coin or any system with known probabilities for its outcomes. The expected surprise (entropy) of a system with $N$ possible outcomes each with probability $p_i$ (all adding up to 1) can be calculated as
\[\begin{align} \sum_{i=1}^{N} p_i \cdot I(p_i) = - \sum_{i=1}^{N} p_i \cdot \text{log}_2(p_i)\label{shannon_entropy}\tag{Shannon entropy}\\ \end{align}\]And notice that if all the $N$ probabilities are the same (so $p_i = \frac{1}{N}$), then the entropy equation can simplify to
\[- \sum_{i=1}^{N} p_i \cdot \text{log}_2(p_i) \Rightarrow \text{log}_2(N)\]Here are some basic examples using $\eqref{shannon_entropy}$.
- The entropy of a fair coin is
- The entropy of a fair 8-sided dice is
- The entropy of an unfair 8-sided dice, where the dice lands on one face $99$% of the time and lands on the other faces the remaining $1$% of the time with equal probability (about $0.14$% each), is
Hopefully it is a bit more intuitive now that entropy represents uncertainty. An 8-sided dice would have higher entropy than a coin since we are more uncertain about the outcome of the 8-sided dice than we are about the coin (8 equally likely outcomes are more uncertain than only 2 equally likely outcomes). But a highly unfair 8-sided dice has less entropy than even a coin since we have very high certainty about the outcome of the unfair dice. Now we have an actual equation to quantify that uncertainty (entropy) about a system.
It is not clear right now how this definition of entropy has anything to do with disorder, heat, or time, but this idea of entropy as uncertainty is fundamental to understanding the entropy of the universe which we will explore shortly. For reference, this definition of entropy is called Shannon entropy.
We will move on now, but I recommend looking further into Information Theory. It has many important direct implications for data compression, error correction, cryptography, and even linguistics, and touches nearly any field that deals with uncertainty, signals, or knowledge.
Physical Entropy
Now we will see entropy from a very different lens, that of Statistical Mechanics. We begin with the tried-and-true introduction to entropy which every student is given.
Balls in a box
I shall give you a box with 10 balls in it, $p_0$ through $p_9$, and we will count how many balls are on the left side of the box and on the right side of the box. Assume every ball is equally likely to be on either side. Immediately we can see it is highly unlikely that we count all the balls are on the left side of the box, and more likely that we count an equal number of balls on each side. Why is that?
Well, there is only one state in which we count all the balls on the left, and that is if every ball is on the left (truly astounding, but stay with me). But there are many ways in which the box is balanced: We could have $p_0$ through $p_4$ one side and the rest on the other, or the same groups but flipped from left to right, or we could have all the even balls on one side and the odd on the other, or again flipped, or any of the other many possible combinations.
This box is a system that we can measure the entropy of, at least once I tell you how many balls are counted on each side. It can take a moment to see, but imagine the box with our left and right counts as a system where the outcome will be finding out where all the individual balls are in the box, similar to rolling a dice and seeing which face it lands on.
This would mean that the box where we count all the balls on the left side only has one possible outcome: all the balls are on the left side. We would take this to mean that this system has $0$ entropy (no expected surprise) since we already know where we will find each individual ball.
The box with balanced sides (5 on each) has many possible equally likely outcomes, and in fact, we can count them. A famous equation in combinatorics is the N-choose-k equation, which calculates exactly this scenario. It tells us that there are 252 possible ways in which we can place 5 balls on each side. The entropy for this system would then be $- \sum_{i=1}^{252} \frac{1}{252} \cdot \text{log}_2(\frac{1}{252}) = \text{log}_2(252) = 7.9772799235$. This is the same as calculating the entropy of a 252-sided dice.
And if we were to increase the number of balls, the entropy of the balanced box would increase since there would then be even more possible combinations that could make up a balanced box.
We should interpret these results as: The larger the number of ways there are to satisfy the large-scale measurement (counting the number of balls on each side), the higher the entropy of the system. When all the balls are on the left, there is only one way to satisfy that measurement and so it has a low entropy. When there are many ways to balance it on both sides, it has high entropy.
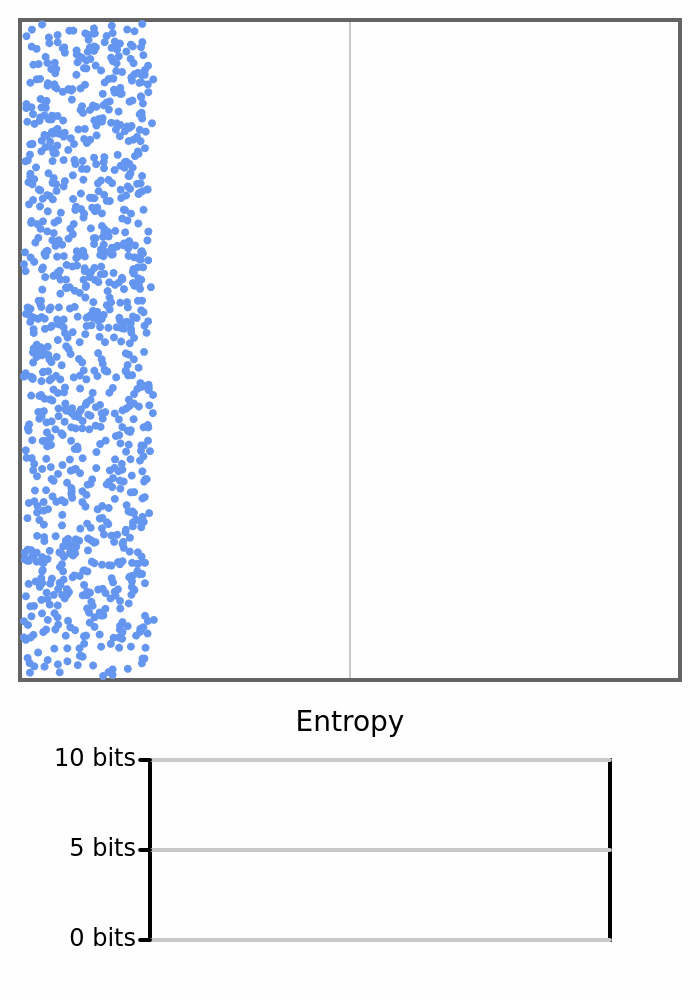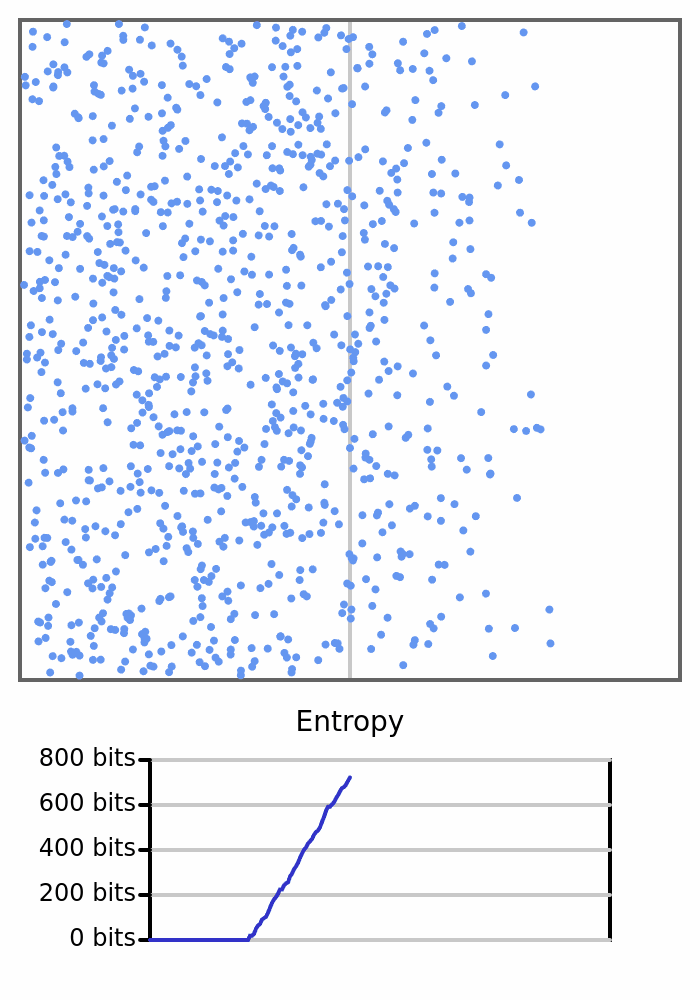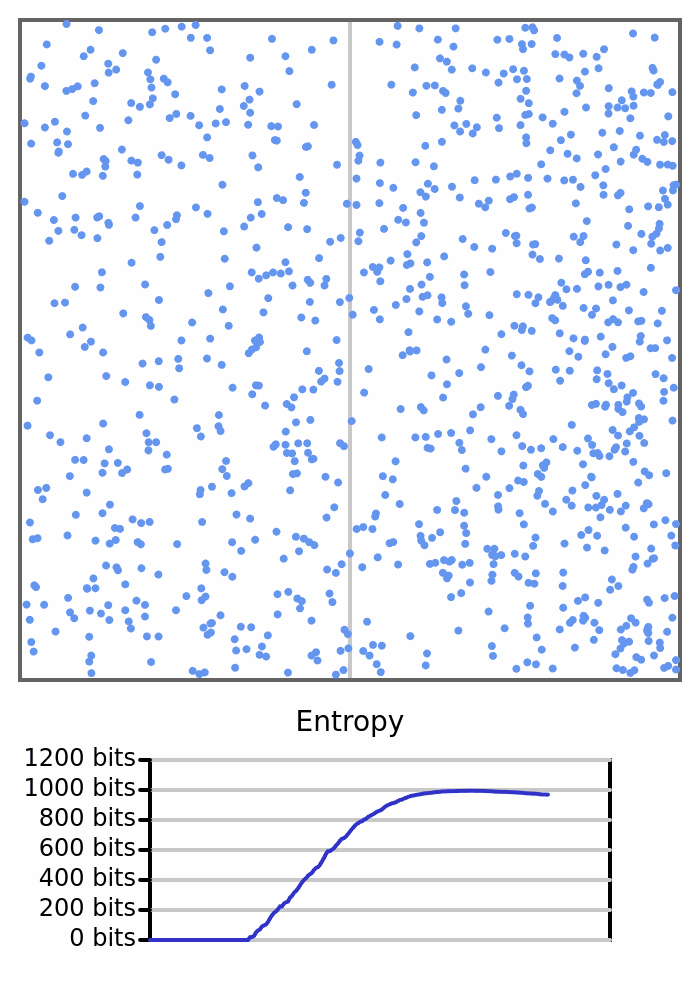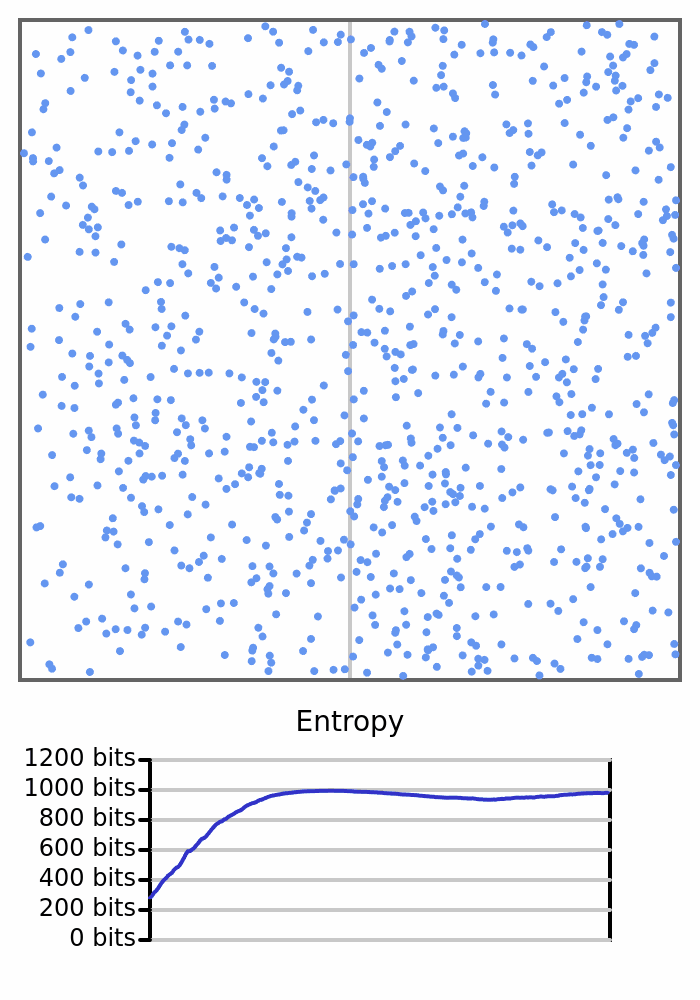
Here we see 1000 balls bouncing around in a box. They will all start on the left, so the box would have 0 entropy, but once the balls start crossing to the right and changing the count on each side, the entropy will increase.
In Statistical Mechanics, the formal term for the large-scale measurement is the macrostate, and the specific states that can satisfy that measurement are microstates. We would call the measurement of the number of balls on each side of the box the macrostate, and the different combinations of positions of individual balls the microstates. So rephrasing the above: There is only one microstate representing the macrostate of all balls being counted on one side, and there are many microstates representing the macrostate of a balanced box.
But why did we decide to measure the number of balls on the left and right? We could have measured a different macrostate, and the entropy would be different.
Macrostates
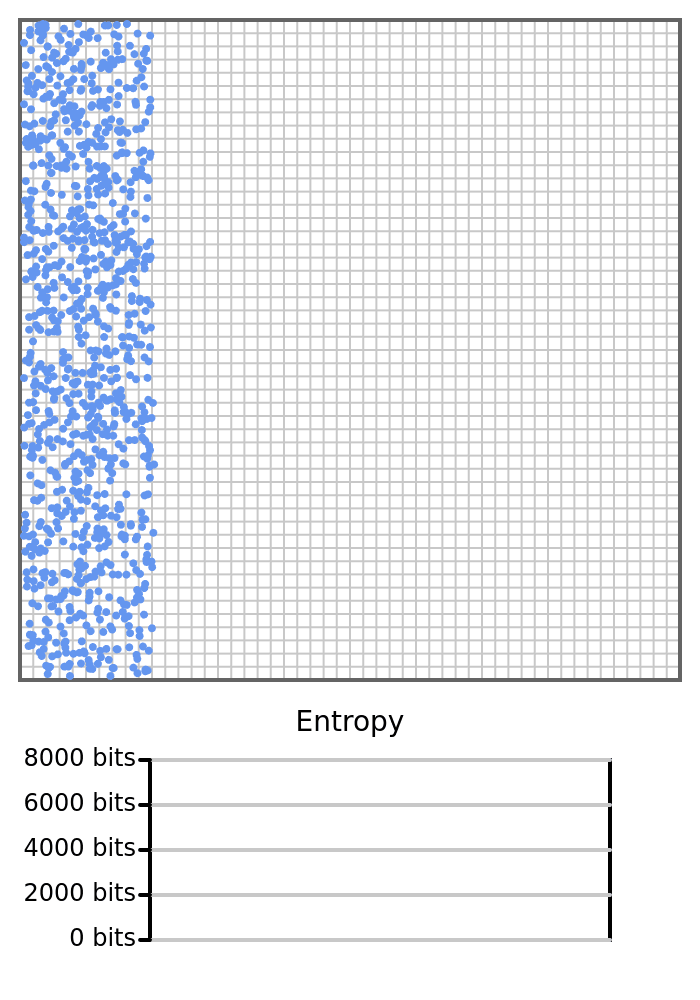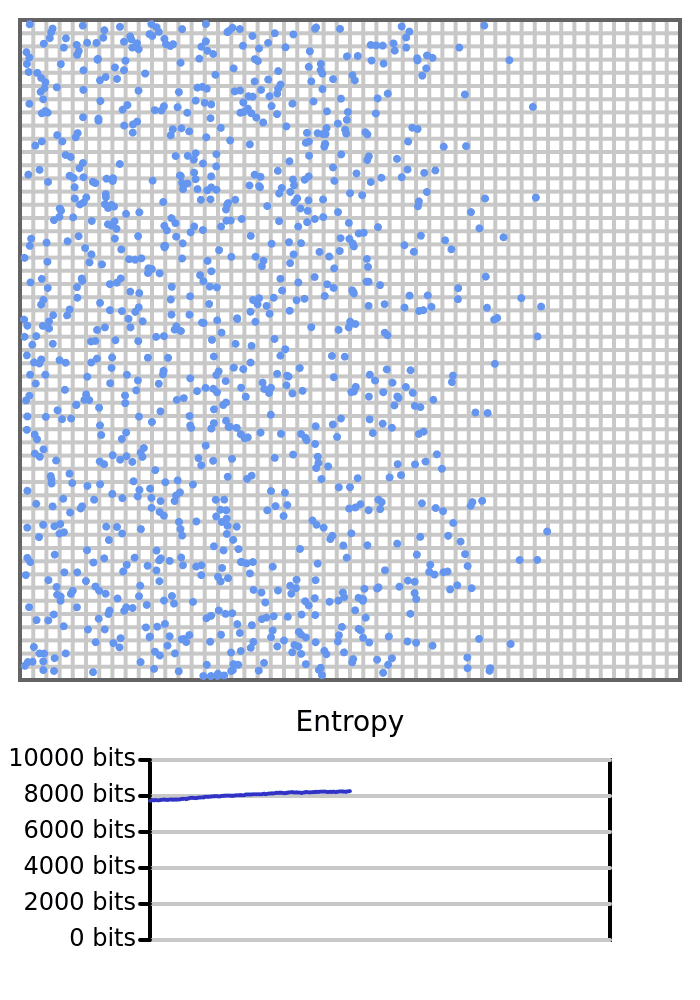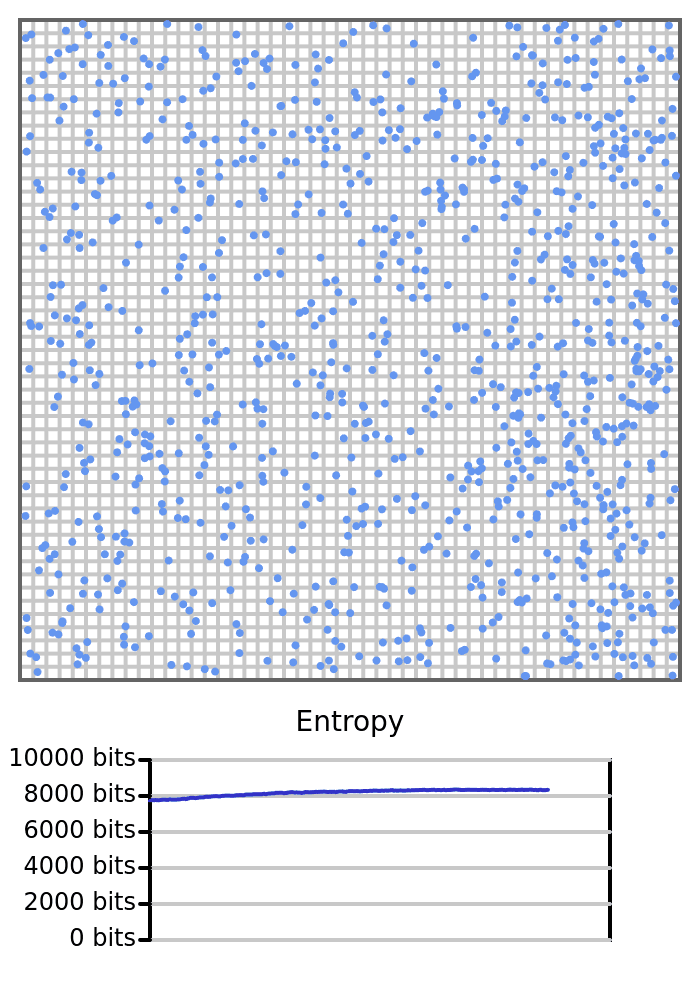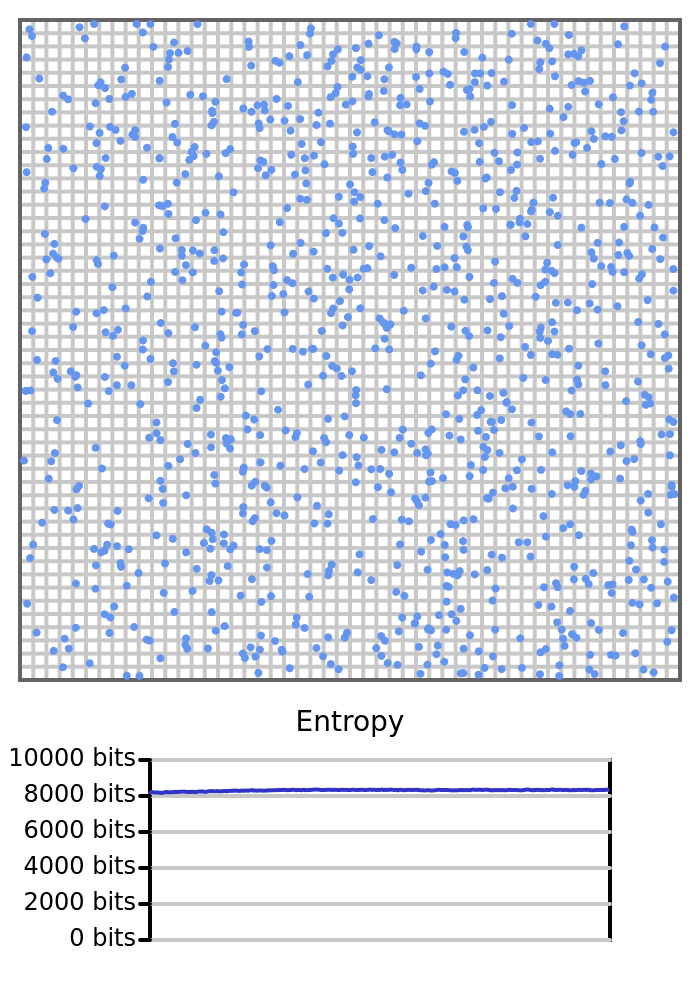
Imagine instead of selecting the left and right halves of the box to count the number of balls, we instead count how many balls are in each pixel of the box. In this scenario, the entropy would almost always be maximized, as the balls rarely share a pixel. Even if all the balls were on the left side of the box, they would likely still each occupy a different pixel, and the measured entropy would be the same as if the balls were evenly distributed in the box.
If we use an expensive instrument to measure the box and track the balls with high precision, then the entropy would rarely change and would be very high. If we instead use an inexpensive instrument that can only tell if a ball is on the left or right of the box, then the entropy will be low and could very easily fluctuate if some of the balls temporarily end up on the same side of the box.
Let’s run exactly the same simulation of 1000 balls in the box again, still starting with the balls on the left. But, this time we count how many balls are in each cell in a 50x50 grid, as opposed to the previous two cells (the left and right cells). The entropy will be high since there are many microstates that represent a bunch of cells with only 1 ball in it, and the entropy won’t change much since two balls rarely share the same cell. Recall that if two balls share the same cell, the count would go up, and there are fewer microstates that satisfy a cell with a count of 2 compared to two cells with a count of 1 in each.
Entropy is not intrinsic to the physical system alone, but rather to our description of it as well — i.e., the macrostate we’re measuring, and the resolution at which we observe it.
This process of measuring a lower-resolution version of our system (like counting how many balls are on the left or right side of a box) is called coarse-graining.
How we choose/measure the macrostate, that is, how we coarse-grain the system, is dependent on the problem we are solving.
- Imagine you have a box of gas (like our balls in a box, but at the scale of $10^{25}$ balls in the box), and we place a temperature-reader on the left and right side of the box. This gives us a macrostate of two counts of the average ball speed on the left and right sides of the box. We can then calculate the entropy by comparing when the temperature-readers are equal to when they are different by $T$ degrees. Once we learn how time and entropy interact, we will use this model to show that the two temperature-readers are expected to converge to the same value over time.
- Imagine you sequence the genome of many different people in a population, you could choose many different macrostates based on what you care about. You could count how many of each nucleotide there are in all the sequences, allowing you to quantify how variable the four nucleotides are in DNA. You could calculate the entropy of every individual position in the DNA sequence by counting how many nucleotide types are used in that position across the population, allowing you to identify portions of DNA that are constant across individuals or vary across individuals.
How you choose to measure the macrostate can come in many forms for the same system, depending on what you are capable of measuring and/or what you care about measuring.
But once we have a macrostate, we need a way to identify all the microstates and assign probabilities to them.
Microstates
When we were looking at the positions of balls in a box in equally sized cells, it was easy to see that every ball was equally likely to be in any of the cells, so each microstate was equally likely. This made calculating the entropy very simple, we just used the simplified version of $\eqref{shannon_entropy}$ to find that for $W$ microstates that satisfy a given macrostate, the entropy of the system is $\text{log}_{2}(W)$. It isn’t too hard to extend this idea to microstates that are not equally likely.
For example, let’s calculate the entropy of a box with 5 balls on the left and 5 balls on the right, but we replace one of the balls in the box with a metal ball that is pulled by a magnet to the left. In this case, the probability of each microstate is no longer equally likely. If we assume there is an $80$% chance that the metal ball is on the left side instead of the right side, then the entropy of the box can be calculated as follows: For all of the 252 microstates, 126 of them have the metal ball on the left, which has a $0.8$ chance of being true, and the other 126 have the metal ball on the right with a $0.2$ chance. This means using the $\eqref{shannon_entropy}$ we get an entropy of
\[- \sum_{i=1}^{126} \frac{0.2}{126} \cdot \text{log}_2(\frac{0.2}{126}) - \sum_{i=1}^{126} \frac{0.8}{126} \cdot \text{log}_2(\frac{0.8}{126}) = 7.69921\]This is a little less than the box with normal balls which had $7.9772799235$ entropy. This is exactly what we should expect, we are a bit more certain about the outcome of this system since we knew where one of the balls was more likely to be.
But this raises a subtle question: why did we choose this particular set of microstates? For example, if we have the macrostate of 5 balls on the left and 5 balls on the right, but we decide to use the 50x50 grid of cells to describe the microstates, then there are far more microstates that satisfy the macrostate compared to when we were using the 2x1 grid of left and right.
Let’s calculate the entropy for those two examples. Keep in mind they both have the same macrostate: 5 balls on the left and 5 balls on the right.
- If we choose to use the microstates of looking at the position of individual balls between two cells splitting the box in half, then we can use n-choose-k to calculate that there are 252 possible combinations of balls across the two cells. This gives us an entropy of $\text{log}_2(252) = 7.977279923$.
- If we choose to use the microstates of looking at the position of individual balls between 50x50 (2500) cells splitting the box into a grid, then we can use n-choose-k to calculate that there are 252 possible combinations of balls across the two halves of the box, for each of which every ball could be in any of 50x25 (1250) cells. This gives us an entropy of $\text{log}_2(252*1250^{10}) = 110.8544037$.
This result lines up very well with our Information-theoretic understanding of entropy: when we allow more microstates to represent the same macrostate, we are more uncertain about the microstate our system is in. But this result does raise some concerns.
If different microstates give different entropy, how do we choose the right microstates for our problem? Unlike the macrostate, this decision of which microstates to use is not determined by our instruments or the scope of the problem, it has to be determined by the person making the calculation. Often for physical systems people will use the set of microstates that capture all the relevant information related to the macrostate. For example, if our macrostate is about balls on the left or right side of a box, then we probably don’t care about the ball’s velocity or mass or anything else but the ball position.
Another concern is that it feels wrong that the same physical system with the same macrostate can have different entropies depending on the microstate representation we use. Usually, we expect physical systems to have invariant measurements regardless of the internal representation we decide to use for our measurement. But this is incorrect for entropy. We need to recall that entropy is the uncertainty of a system and that the definition of entropy is completely dependent on what we are uncertain about, which for physical systems are the microstates. This would be similar to someone asking “How many parts make up that machine?”, to which we should respond “How do you define a ‘part’?”. When we ask “What is the entropy of this macrostate?”, we need to respond with “What microstates are we using?”.
With all that said, there is some small truth to what our intuition is telling us, although it doesn’t apply to the general case. While the entropy of the system changes when we change the microstates, the relative differences in entropy across macrostates will be equal if the new microstates uniformly multiply the old microstates. That is, if each original microstate is split into the same number of refined microstates, then the entropy of every macrostate increases by a constant. We’re getting lost in the terminology, an example will demonstrate.
Let us again take the 10 balls in a box, and we will calculate the entropy of the system for a few different macrostates and microstate representations. We indicate the number of balls on each side of the box with (L, R), where L is the number of balls on the left and R is the number of balls on the right. Then we calculate the entropy using the microstate of a 2x1 grid of cells (just the left and right halves of the box) and for the 50x50 grid of cells.
| (10,0) | (9,1) | (8,2) | (7,3) | (6,4) | (5,5) | (4,6) | (3,7) | (2,8) | (1,9) | (0,10) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2x1 | 0.00000 | 3.32193 | 5.49185 | 6.90689 | 7.71425 | 7.97728 | 7.71425 | 6.90689 | 5.49185 | 3.32193 | 0.00000 |
| 50x50 | 102.87712 | 106.19905 | 108.36898 | 109.78401 | 110.59137 | 110.85440 | 110.59137 | 109.78401 | 108.36898 | 106.19905 | 102.87712 |
And if we look, we will see that the entropy in the 50x50 grid microstate values is just the 2x1 grid values plus a constant. The relative entropy in both cases would be identical. This is even more clear if we mathematically show how the entropy is calculated. For the 2x1 grid we use the equation $\text{log}_2({10 \choose L})$, and for the 50x50 grid we use $\text{log}_2(1250^{10} {10 \choose L}) = \text{log}_2(1250^{10}) + \text{log}_2({10 \choose L})$. Mathematically we can see that it is the same as the entropy of the 2x1 grid offset by $\text{log}_2(1250^{10})$.
You can imagine if we added another dimension along the microstates that we would increase the entropy again by a constant. For example, if each of the 10 balls could be one of 3 colors, then the number of microstates would grow by a factor of $3^{10}$, and so the entropy of the whole system would increase by $\text{log}_2(3^{10})$.
Our intuition was correct when we used different microstates that are multiples of each other, but that intuition fails if the microstates are not so neatly multiples of each other. An easy example of this is if we represent the left side of the box as one cell and the right as a 50x25 grid of cells, then the entropy looks very different. Below is the table again, but with the added row of our non-homogenous microstates. An example of how we calculate the entropy of macrostate $(3, 7)$ is: there are 120 equally likely ways to place 3 balls on the left and 7 balls on the right, but the balls on the right can also be in $1250^7$ different states, so the entropy is $\text{log}_2(120 \cdot 1250^7) = 78.920877252$.
| (10,0) | (9,1) | (8,2) | (7,3) | (6,4) | (5,5) | (4,6) | (3,7) | (2,8) | (1,9) | (0,10) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2x1 | 0.00000 | 3.32193 | 5.49185 | 6.90689 | 7.71425 | 7.97728 | 7.71425 | 6.90689 | 5.49185 | 3.32193 | 0.00000 |
| 50x50 | 102.87712 | 106.19905 | 108.36898 | 109.78401 | 110.59137 | 110.85440 | 110.59137 | 109.78401 | 108.36898 | 106.19905 | 102.87712 |
| mixed | 0.00000 | 13.60964 | 26.06728 | 37.77003 | 48.86510 | 59.41584 | 69.44052 | 78.92088 | 87.79355 | 95.91134 | 102.87712 |
A funny thing to note is that when all the balls are on the left, the entropy is zero, but when all the balls are on the right, the entropy is maximized. And again, hopefully, this makes sense from our understanding of entropy, that it measures uncertainty relative to our microstates. If we know all the balls are on the left, then we know they must be in the single left cell, so no uncertainty. If we know the balls are all on the right, then they could be in any of $1250^{10}$ microstates, so high uncertainty.
Clearly, we need to be careful and aware of what microstates we are choosing when measuring the entropy of a system. Fortunately, for most physical systems we use the standard microstates of a uniform grid of positions and momentums of the balls (particles) in the system. Another standard microstate to use is the continuous space of position and momentum.
Continuous Microstates
So far, we’ve looked at discrete sets of microstates — such as balls in cells. But in physical systems, microstates are often continuous: positions and momenta can vary over a continuum. How do we compute entropy in this setting? This is not related to the rest of the explanation, but it is an interesting tangent to explore.
Let’s return to our 10 balls in a 2D box. If each ball can occupy any position in the square, then the microstate of the system is a point in a $20$-dimensional space (2 dimensions per ball). The number of possible microstates is infinite — and each individual one has infinitesimal probability.
In this setting, we use a probability density function $\rho(x)$, and entropy becomes a continuous integral:
\[S = - \int_X \rho(x) \log_2 \rho(x) \, dx\]This is called differential entropy. It generalizes Shannon entropy to continuous systems, though it has some subtleties — it can be negative, and it’s not invariant under coordinate transformations.
If the density is uniform, say $\rho(x) = \frac{1}{V}$ over a region of volume $V$, then the entropy becomes:
\[S = - \int_X \frac{1}{V} \log_2 \left( \frac{1}{V} \right) dx = \log_2(V)\]So entropy still grows with the logarithm of the accessible state volume, just as in the discrete case.
This formalism is particularly natural in quantum mechanics, where the wavefunction $\psi(x)$ defines a probability density $\rho(x) = |\psi(x)|^2$. Consider a 1D Gaussian wavefunction:
\[\psi(x) = \left( \frac{1}{\pi \sigma^2} \right)^{1/4} e^{-x^2 / (2 \sigma^2)}\]Its entropy (in bits) is:
\[S = - \int_{-\infty}^{\infty} \rho(x) \log_2 \rho(x) \, dx = \frac{1}{2} \log_2(2 \pi e \sigma^2)\]This shows that wider distributions have higher entropy, as expected: a more spread-out wavefunction indicates more uncertainty in the particle’s location.
For instance:
- If $\sigma = 1$, then $S \approx 2.047$
- If $\sigma = 3$, then $S \approx 3.600$
Which again should make sense: When we are less certain about a system, like where a particle will be when measured, the more entropy it has.
And a quick issue to address: If the state space is unbounded, like momentum in classical mechanics, then the entropy can diverge. This isn’t a problem in practice because physical systems typically have probability distributions (like Gaussians) that decay quickly enough at infinity to keep the entropy finite. When that’s not the case, we either limit the system to a finite region or focus on entropy differences, which remain well-defined even when absolute entropy diverges.
But let’s get back to our main topic, and we’ll get back into it with a historical overview.
Standard Usage of Entropy
Eighty years before Claude Shannon developed Information Theory, Ludwig Boltzmann formulated a statistical definition of entropy for an ideal gas. He proposed that the entropy $S$ of a system is proportional to the logarithm of the number of microstates $W$ consistent with a given macrostate:
\[\begin{align} S = k_{B} \ln(W) \label{boltzmann_entropy}\tag{Boltzmann entropy} \end{align}\]This equation should look familiar: it’s the equal-probability special case of the Shannon entropy we’ve been using, just with a change of base (from $\log_2$ to $\ln$) and a scaling factor $k_B$ (Boltzmann’s constant). The connection between Boltzmann’s statistical mechanics and Shannon’s information theory is more than historical coincidence—both quantify uncertainty, whether in physical states or messages.
A few years later, Josiah Willard Gibbs generalized Boltzmann’s definition to cases where microstates are not equally likely. His formulation remains the standard definition of entropy in modern physics:
\[\begin{align} S = -k_B \sum_{i} p_i \ln(p_i) \label{gibbs_entropy}\tag{Gibbs entropy} \end{align}\]This is formally identical to Shannon entropy, again differing only in logarithm base and physical units. But Gibbs’s generalization was a profound leap: it enabled thermodynamics to describe systems in contact with heat baths, particle reservoirs, and other environments where probability distributions over microstates are non-uniform. This made entropy applicable far beyond ideal gases—covering chemical reactions, phase transitions, and statistical ensembles of all kinds.
Now that we have a formal understanding of entropy with some historical background, let’s try to understand how entropy relates to our universe and in particular to time.
Time
How does time play a role in all of this?
When you drop a spot of milk into tea, it always spreads and mixes, and yet you never see the reverse where the milk molecules spontaneously separate and return to a neat droplet. When ocean waves crash into the shore, the spray and foam disperse, but we never see that chaos reassemble into a coherent wave that launches back into the sea. These examples are drawn from this lecture on entropy by Richard Feynman. If you were shown a reversed video of these events, you’d immediately recognize something was off. This sounds obvious at first, but it actually isn’t clear this should be true if we just look at the laws of physics. All the known laws of physics are time-reversible (the wave function collapse seems to be debatable), which just means that they do look the same playing forward and backward. The individual molecules all obey these time-reversible laws, and yet the cup of tea gets murky from the milk always mixing in.
This highlights a fundamental paradox: the microscopic laws of physics are time-reversible, but the macroscopic world is not. If you took a video of two atoms bouncing off each other and played it backward, it would still look physically valid, but play a video of milk mixing into coffee backward, and it looks obviously wrong.
We want to build a simplified model of time in a way that reflects both the time-reversibility of microscopic laws and the time-asymmetry of macroscopic behavior. Let’s imagine the complete state of a physical system, like a box of particles, as a single point in a high-dimensional space called phase space, with each dimension corresponding to a particle’s position and momentum. As time evolves, the system traces out a continuous trajectory through this space.
The laws of physics, such as Newton’s equations, Hamiltonian mechanics, or Schrödinger’s equation, all govern this trajectory. They are deterministic and time-reversible. That means if you reverse the momenta of all particles at any moment, the system will retrace its path backward through state space.
So far everything is time-reversible, including this view of how the universe moves through time. But we will see that even in this toy model, time appears to have a preferred direction, an arrow of time.
The key lies in coarse-graining. When we observe the world, we don’t see every microscopic detail. Instead, we measure macrostates: aggregate properties like temperature, pressure, position of an object, or color distribution in a cup of tea. Each macrostate corresponds to many underlying microstates — and not all macrostates are created equal.
For example, consider a box sliding across the floor and coming to rest due to friction. At the microscopic level, the system is just particles exchanging momentum, and all time-reversible. But we certainly would not call this action time-reversible, we never see a box spontaneously start speeding up from stand-still. But, if we took the moment after the box comes to a rest due to friction, and you reversed the velocities of all the particles (including those in the floor that absorbed the box’s kinetic energy as heat), the box would spontaneously start moving and slide back to its original position. This would obey Newton’s laws, but it’s astronomically unlikely. Why?
The number of microstates where the energy is spread out as heat (the box is at rest, and the molecules in the floor are jiggling) vastly outnumber the microstates where all that energy is coordinated to move the box. The stand-still macrostate has high entropy while the spontaneous-movement macrostate has low entropy. When the system evolves randomly or deterministically from low entropy, it is overwhelmingly likely to move toward higher entropy simply because there are more such microstates.
If you had perfect knowledge of all particles in the universe (i.e., you lived at the level of microstates), time wouldn’t seem to have a direction. But from the perspective of a coarse-grained observer, like us, entropy tends to increase. And that’s why a movie of tea mixing looks natural, but the reverse looks fake. At the level of physical laws, both are valid. But one is typical, and one is astronomically rare, all because we coarse-grained.
To drive the point home, let’s again look at the balls in a box. We’ll define macrostates by dividing the box into a grid of cells and counting how many balls are in each bin.
Now suppose the balls move via random small jitters (our toy model of microscopic dynamics). Over time, the system will naturally tend to explore the most probable macrostates, as the most probable macrostates have far more microstates for you to wander into. That is, entropy increases over time, not because of any fundamental irreversibility in the laws, but because high-entropy macrostates are far more typical.
If we started the simulation with all the balls packed on the left, that’s a very specific (low entropy) macrostate. As they spread out, the number of compatible microstates grows, and so does the entropy.
This leads to a crucial realization: Entropy increases because we started in a low-entropy state. This is often called the Past Hypothesis, the postulate that the universe began in an extremely low-entropy state. Given that, the Second Law of Thermodynamics follows naturally. The arrow of time emerges not from the dynamics themselves, but from the statistical unlikelihood of reversing them after coarse-graining, and the fact that we began in a low-entropy state.
You could imagine once a system reaches near-maximum entropy that it no longer looks time-irreversible. The entropy of such a system would fluctuate a tiny bit since entropy is an inherently statistical measure, but they would be small enough not to notice. For example, while it is clear when a video of milk being poured into tea (a low-entropy macrostate) is playing forward as opposed to backward, you couldn’t tell if a video of already-combined milk and tea (a high-entropy macrostate) being swirled around is playing forward or backward.
While there are tiny fluctuations in entropy, they are not enough to explain the large-scale phenomena that sometimes seem to violate this principle that we just established of entropy always increasing with time.
Violations of the Second Law?
Some real-world examples seem to contradict the claim that entropy always increases. For instance, oil and water separate after mixing, dust clumps into stars and planets, and we build machines like filters and refrigerators that separate mixed substances. Aren’t these violations?
The issue is we have only been considering the position of molecules, while physical systems have many different properties which allow for more microstates. For example, if we start considering both the position and velocity of balls in a box, then the entropy can be high even while all the balls are on the left side of the box since every ball could have a different velocity. If the balls were all on the left and the velocities were all the same, then the entropy would be low. Once we consider velocity as well, entropy can increase both from more spread out positions and more spread out velocities.
When water and oil separate, the positions of the molecules separate into top and bottom, which appears to decrease positional entropy. However, this separation actually increases the total entropy of the system. Why? Water molecules strongly prefer to form hydrogen bonds with other water molecules rather than interact with oil molecules. When water molecules are forced to be near oil molecules in a mixed state, they must adopt more constrained arrangements to minimize unfavorable interactions, reducing the number of available microstates. When water and oil separate, water molecules can interact freely with other water molecules in more configurations, and oil molecules can interact with other oil molecules more freely. This increase in available microstates for molecular arrangements and interactions more than compensates for the decrease in positional mixing entropy. So, while the entropy decreases if we only consider the general positions of molecules (mixed versus separated), the total entropy increases when we account for all the molecular interactions, orientations, and local arrangements. This demonstrates why we need to consider all properties of a system when calculating its entropy.
When stars or planets form together from dust particles floating around in space and clump together from gravity, it would seem that even when we consider position and velocity of the particles that the entropy might be decreasing. Even though the particles speed up to clump together, they slow down after they collide, seemingly decreasing entropy. This is because we are again failing to consider the entire system. When particles collide with each other, their speed decreases a bit by turning that kinetic energy into radiation, causing photons to get sent out into space. If we considered a system where radiation isn’t allowed, then the kinetic energy would just get transferred from one particle to another through changes in velocity, and the entropy of the system would still be increasing because of the faster velocities. Once we start considering the entropy of the position, velocity, and all particles in a system, we can consider all the microstates that are equally likely and calculate the correct entropy.
Similarly, once we consider the entire system around a refrigerator, the decrease in entropy disappears. The entropy from the power generated to run the refrigerator and the heat moved from the inside to the outside of the refrigerator will offset the decrease in entropy caused by cooling the inside of the refrigerator. Local decreases in entropy can be generated, as long as the entropy of the entire system is still increasing.
Ensure that the entire system is being considered when analyzing the entropy of a system, with the position, velocity, other interactions of particles, that all particles are included, and that the entire system is actually being analyzed.
Disorder
Entropy is sometimes described as “disorder,” but this analogy is imprecise and often misleading. In statistical mechanics, entropy has a rigorous definition: it quantifies the number of microstates compatible with a given macrostate. That is, entropy measures our uncertainty about the exact microscopic configuration of a system given some coarse-grained, macroscopic description.
So where does the idea of “disorder” come from?
Empirically, macrostates we label as “disordered” often correspond to a vastly larger number of microstates than those we consider “ordered”. For example, in a child’s room, there are many more configurations where toys are scattered randomly than ones where everything is neatly shelved. Since the scattered room corresponds to more microstates, it has higher entropy.
But this connection between entropy and disorder is not fundamental. The problem is that “disorder” is subjective—it depends on human perception, context, and labeling. For instance, in our earlier example of 1000 balls bouncing around a box, a perfectly uniform grid of balls would have high entropy due to the huge number of possible microstates realizing it. And yet to a human observer, such a grid might appear highly “ordered.”
The key point is: entropy is objective and well-defined given a macrostate and a set of microstates, while “disorder” is a human-centric heuristic concept that sometimes, but not always, tracks entropy. Relying on “disorder” to explain entropy risks confusion, especially in systems where visual symmetry or regularity masks the underlying statistical structure.
Conclusion
So here are some thoughts in regard to some common statements made about entropy:
- Entropy is a measure of disorder.
- “disorder” is a subjective term for states of a system that humans don’t find useful/nice, and usually has much higher entropy than the “ordered” macrostate that humans create. Because of this, when entropy increases, it is more likely that we end up in disordered state, although not guaranteed.
- Entropy always increases in a closed system.
- This is a statistical statement that for all practical purposes is true, but is not guaranteed and can fail when you look at very small isolated systems or measure down to the smallest details of a system. It also assumes you started in a low-entropy state, giving your system space to increase in entropy. This has the neat implication that since our universe has been observed to be increasing in entropy, it must have begun in a low-entropy state.
- Heat flows from hot to cold because of entropy.
- Heat flows from hot to cold because the number of ways in which the system can be non-uniform in temperature is much lower than the number of ways it can be uniform in temperature, and so as the system “randomly” moves to new states, it will statistically end up in states that are more uniform.
- Entropy is the only time-irreversible law of physics.
- All the fundamental laws of physics are time-reversible, but by coarse-graining and starting from a lower-entropy state, a system will statistically move to a higher-entropy state. This means if a system is already in a near-maximum entropy state (either because of its configuration or because of the choice for coarse-graining) or we don’t coarse-grain, then entropy will not look time-irreversible.
And here is some further reading, all of which I found supremely helpful in learning about entropy.