Dynamic Decentralized Cluster Size Estimation

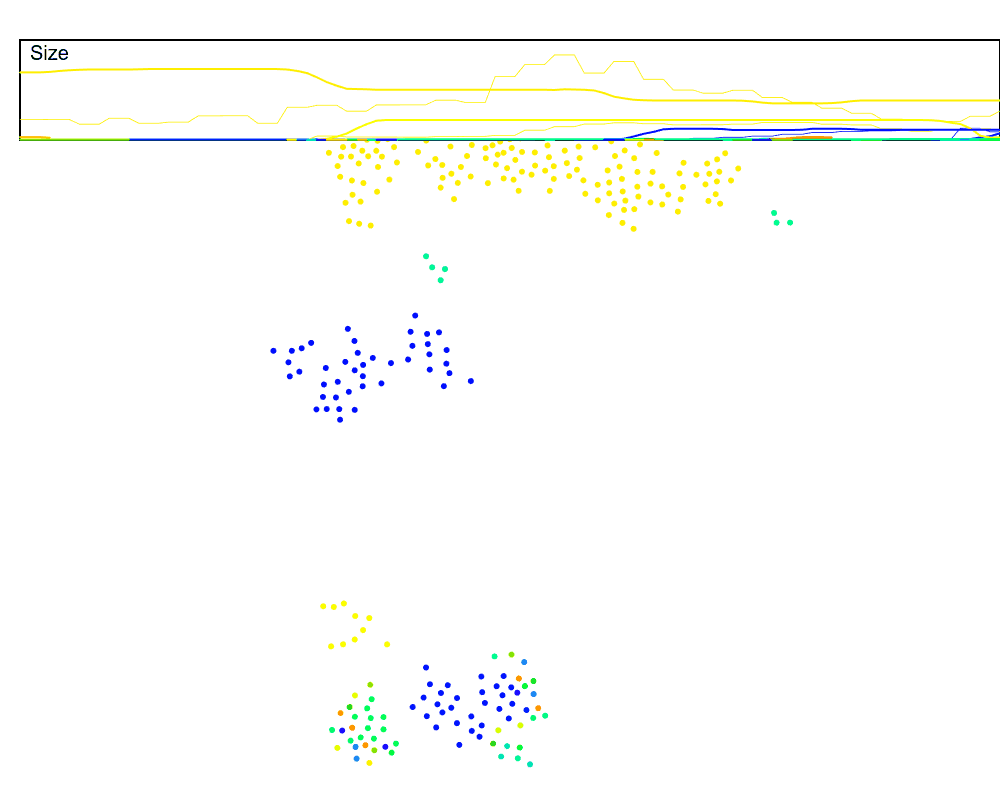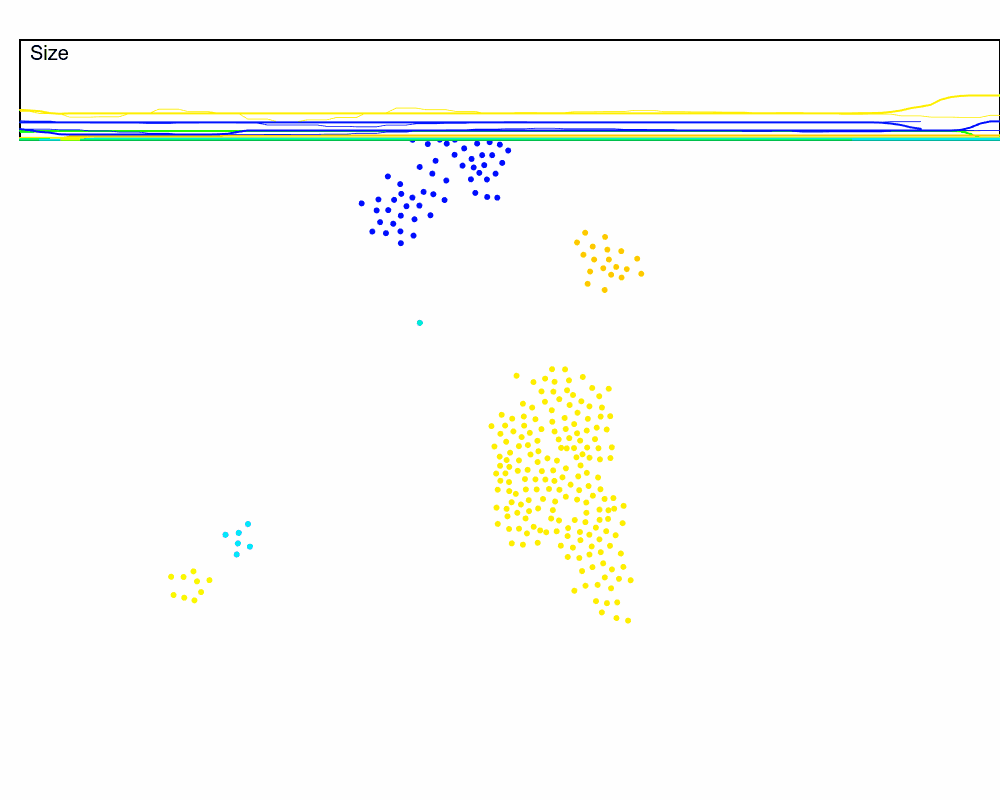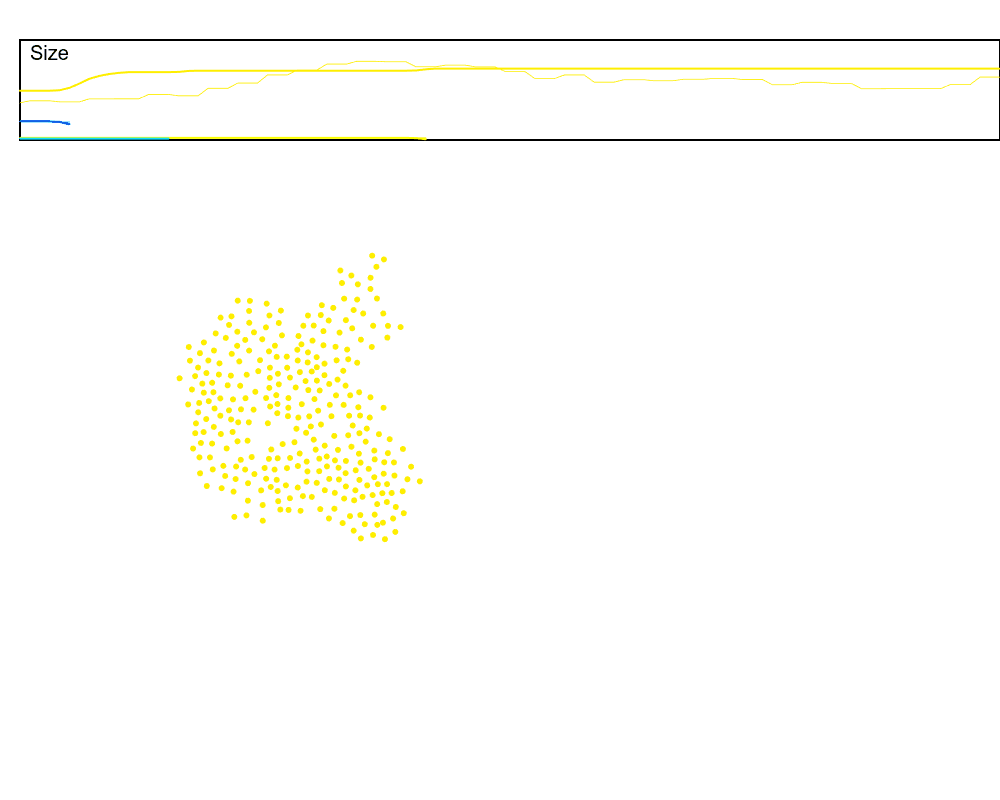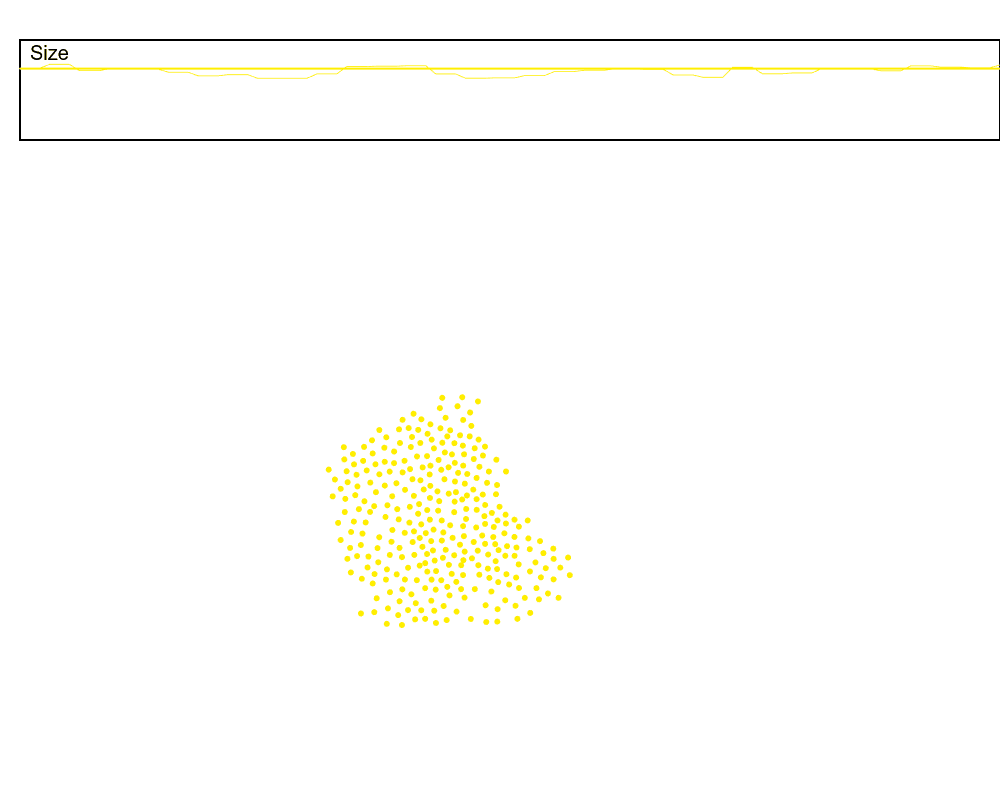
We previously designed a cluster ID algorithm to dynamically identify clusters (connected components) of MANETs, but it had some issues. The main issue was that a single node was capable of changing the ID of a large cluster when it joined, while it would be more natural to have the largest cluster win a merge. This means we need a size-estimation algorithm.

Recap

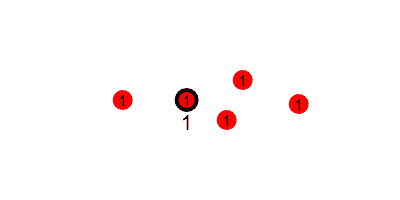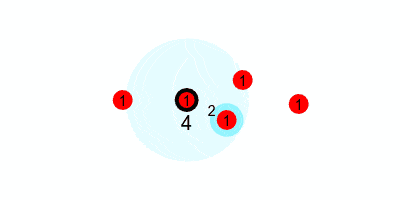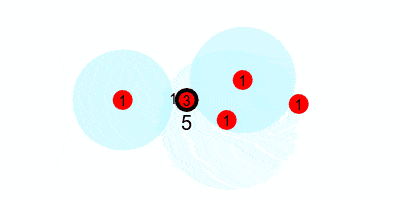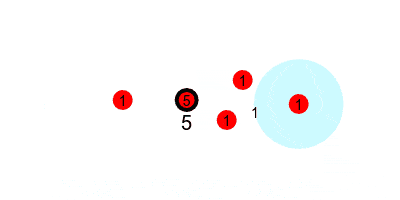
A recap of the cluster ID algorithm:

onceASecond():
    if isLeader:
        broadcastClusterID()
    else:
        if noReceivesInLongTime():
            isLeader = true
            currentClusterID = randomNumber()

onReceiveClusterID(incomingClusterID):
    if incomingClusterID > currentClusterID:
        currentClusterID = incomingClusterID
        if isLeader:
            isLeader = false
    if incomingClusterID == currentClusterID:
        broadcastClusterID()

You can see now how even small clusters can change the cluster ID of a very large cluster. It would be far more natural to have the largest cluster take over the smaller clusters. That requires every node knows its cluster size. If we can do that, then we just have to modify line 10 of the pseudocode to compare cluster sizes instead of cluster IDs. So how can we calculate cluster sizes such that every node knows the value, and can we make it dynamic with cluster size changes?

Here are some classic approaches to size estimation in networks:

• Flood-based: Every node flood-fills the network with their unique ID and everyone counts how many IDs they saw. This is not at all scalable.
• Push-sum: A diffusion-based approach that conserves values as they diffuse across the swarm, until you can derive the swarm size based on how diffused the value was. This is not dynamic (at least not for nodes leaving a swarm), and is very slow. It is interesting though, and there are many other diffusion-based protocols that solve different problems.
• Token-Passing: A counter is passed around that gets incremented for every new node it sees. This is not dynamic and requires knowledge of the entire topology. Or you can use probabilistic methods, but these are slow.
• Population protocols: A fascinating class of algorithms that assume the bare minimum of its agents, allowing for highly general algorithms. Population protocols assume random interactions, which is not our environment, but there are still useful population protocols for size estimation.

But none of these exactly fit our specific environment, so let’s develop our own solution! Although, this master’s thesis is very close to what we will eventually develop.

Leader as a root

First, we should notice that the current algorithm allows the leader to very quickly spread information to the rest of the swarm by tagging that information to its keep-alive message. This means we can focus on just estimating the swarm size at the leader. This simplifies the problem to “How can the leader estimate the cluster size of a MANET?”.

Our approach will have each node send $1$ to the leader, and the leader can take a sum to calculate the swarm size. But we don’t have any routing information in this network, so we need some additional information.

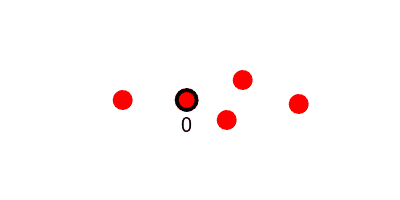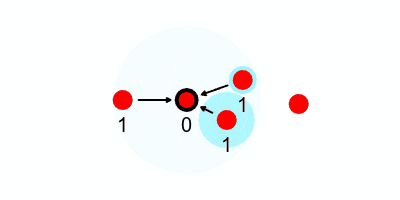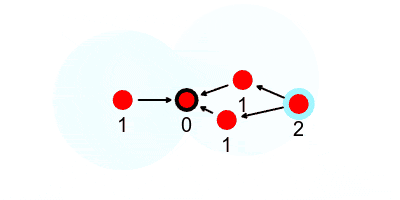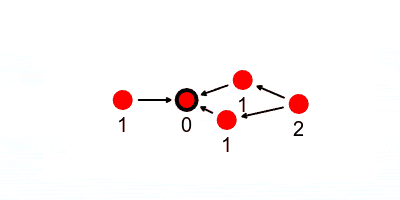
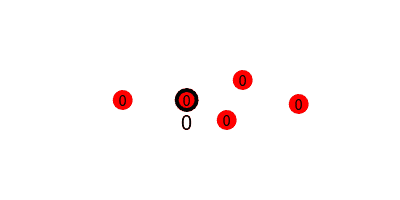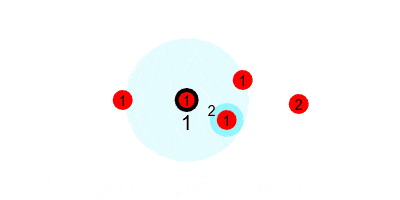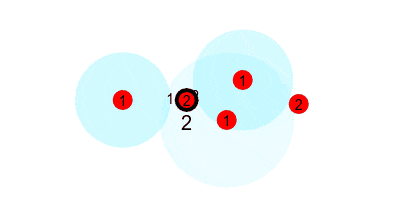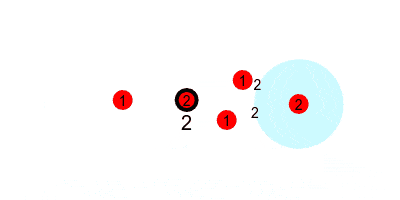
As the keep-alive message travels through the swarm, it can carry an incrementing counter which counts how many hops a node is from the leader. For example, the initial message from the leader has a counter of 1 since anyone who hears that message is one hop from the leader, and the counter is incremented as it gets passed along. If a node hears multiple messages with different hop-counts, it should use the smallest.

If a node keeps track of its neighbors and their hop-counts (which it can do since every node will have a broadcast in a flood-fill), then it also will know which nodes to send a message to in order to send information closer to the leader. Below we see arrows indicating who a node can send to in order to send messages closer to the leader, which is derived from a neighbor list it generates every communication round.

And now every node can pass its value of $1$ to the leader by passing it to a neighbor that’s one hop closer to the leader, and keep passing until all the values make their way to the leader. There are a number of ways we could do this.

The easiest way is to have each node pick a single neighbor that’s closer to the leader, and pass its value to them. This requires every node to have a unique ID, which is somewhat undesirable. If we wanted to avoid using IDs, we could have each node count how many neighbors it has that are closer to the leader, say $N$ neighbors, and broadcast $\frac{1}{N}$ with the requirement that only people who are closer to the leader can receive the message. This would mean that $N$ nodes would each receive $\frac{1}{N}$, and when all of the values eventually make their way to the leader, they’ll still add up to the number of nodes in the swarm.

Here’s an issue, though: the above routing really does not work well in dynamic swarms.

Dynamic swarms

When nodes are moving, the neighbors for each node will change every round, causing the neighbor lists to be out of date. This means you often won’t be sending $\frac{1}{N}$ to $N$ nodes, and the eventual sum becomes inaccurate. We could require acknowledgments, but it is far easier and just as reliable to instead send your message to the node most recently heard from. This does require node IDs, or at least a nonce for the broadcast so the sender can address the message. Below we see the routing information using the first node you hear every communication round. This means that although a node may leave your range within a communication round, you can be certain the node will hear the immediate response, as you just heard their broadcast.

This will re-build a leader-rooted tree every communication round. Because it’s fun to see, let’s visualize the rooted trees of a large swarm in a highly dynamic environment.

This is good, the routing tables now handle dynamic changes. Now let’s add in the summing for the size estimation.

First, we look at how the $1$s are passed along the tree. If every node starts with $1$, and passes it to their nearer neighbor every round, this is what it would look like.

But we want to run this counting protocol every round (so it can adapt to changes in swarm size), so we will have each node send $1$ every round. This requires that every node add any incoming values to their current value, and reset the accumulated value to $1$ after each round. That would look like the following, where we update the estimated sum (printed under the leader) at the end of every round.

This can easily be used for summing more than just the swarm size, such as summing sensor data (or most generally reducing any commutative semigroup). You could also send both the node counts and the sensor data st the same time, then divide the sums at the leader to calculate averages.

The reason it takes a few rounds to reach the correct estimate is that it takes $N$ rounds for a message to reach the leader from $N$ hops away. So the initial estimate is $1$ since the leader hasn’t heard from any other nodes. After the first communication round the messages from the three $1$-hop nodes reach the leader and the estimate increases to $4$. After the second communication round the messages from the one $2$-hop node reaches the leader, and now the estimate is correct. Similarly, if the $2$-hop node leaves the swarm, it will take $2$ communication rounds for the estimate at the leader to decreases by $1$.

Let’s run this in the dynamic setting, but speed up the rate at which the keep-alive signal is sent, which should compensate for the $N$ hops delay from far-away nodes. We will also plot the estimated swarm size (the thin lines) against the true swarm size (thick lines) to see how accurate this is. And we can use our size estimation in the cluster merges now!

Hmmm, it mostly works, but it’s also pretty noisy. Why?

In a dynamic swarm, values that are initially $N$ hops away may not always take $N$ hops to reach the leader. This means part of the sums may arrive a few rounds too early or too late. For example, if a node has the accumulated value of $5$, but jumps from being three hops away to being two hops away, then those $5$ counts will reach the leader one hop earlier than expected, and one round will have an extra $5$ while the next round will be missing $5$.

A naive way to account for this is to keep a rolling average at the leader. I also tried a Kalman filter, but actually found better results with the rolling average. There is certainly a better signal processing technique for this specific scenario, but for now the rolling average works well enough. Let’s look at a rolling window size that averages over the last 5 communication rounds.

Much better. But why 5 rounds? This gives us a great excuse to track another feature of the swarm, the radius. In order to dynamically set the window of our rolling average, we want to know how noisy the sum will be, which can be roughly approximated by the radius of the cluster.

Radius estimation

The radius of a cluster is defined to be the number of hops that the farthest node is from its leader.

Sending this value to the leader is actually much easier than calculating the sum of the swarm. Each node sends their hop-count to the leader, and it can be reduced along the way by always taking the $MAX$. When reducing with $+$ for the size, the total sum across the swarm had to be preserved (which is hard due to duplicated or dropped messages), but with $MAX$, we just need to ensure the largest value makes it to the leader. We can get rid of ID-based routing and the tree generation since we don’t care about duplicated messages, and we can instead attach a requirement to each broadcast for how low the receivers’ hop-count must be. And we don’t want to reset each node to $1$ every round like we did for the size; instead, we reset each node to its current hop count (since that is the largest hop count it has seen this round).

The following animation is somewhat misleading since, again, these broadcasts are not being addressed to any particular nodes. I have animated it so we see the max seen hop count get sent to the nodes that meet the requirement to have a lower hop-count than the sender, but keep in mind that no ID-based routing was necessary.

Bringing it all together

By running the size estimation and radius estimation at the same time (they can be combined into a single broadcast), the leader can get a constant stream of size estimations and radii, then use the radius to determine the window size when averaging the sizes. We then use this final size estimate when comparing clusters to determine which one will win a merge.

I find it fun that we relied on the original cluster ID algorithm to elect a leader, which was then used for size estimation, which is now being used to improve the cluster ID algorithm. Let’s watch a live simulation, where we should see the smaller clusters are always subsumed by the larger clusters.

The code for the above animation and some of the other animations can be found here.

And the pseudocode is below, which maps almost exactly to the code running the animation above. This is for the instance where we assume unique node IDs exist, and the tree generation uses the node most recently heard from.

onceEveryInterval():
    if isClusterLeader:
        broadcastClusterMessage(
            clusterIdentifier       = myClusterIdentifier,
            roundIdentifier         = newRoundIdentifier(),
            senderIdentifier        = myNodeIdentifier,
            distanceToLeader        = 1,
            estimatedSize           = currentEstimatedSize,
            sizeContribution        = 0,
            receiverIdentifier      = null,
            radiusContribution      = 0,
            receiverMaximumDistance = 0
        )
        resetLocalRoundData()

    else if timeOutWithoutReceiving():
        isClusterLeader     = true
        myClusterIdentifier = generateNewIdentifier()
        resetLocalRoundData()

onReceiveClusterMessage(msg):
    if msg.clusterIdentifier != myClusterIdentifier:
        // Merge only if strictly larger or tie + bigger ID
        if (msg.estimatedSize < currentEstimatedSize) or
           ((msg.estimatedSize == currentEstimatedSize) and
            (msg.clusterIdentifier <= myClusterIdentifier)):
            return
        myClusterIdentifier    = msg.clusterIdentifier
        isClusterLeader        = false
        distanceToLeader       = msg.distanceToLeader
        localSizeAccumulator   = 1
        localRadiusAccumulator = distanceToLeader

    if msg.receiverIdentifier == myNodeIdentifier:
        localSizeAccumulator += msg.sizeContribution

    if distanceToLeader < msg.receiverMaximumDistance:
        localRadiusAccumulator = max(localRadiusAccumulator, msg.radiusContribution)

    if roundIsNew(msg.roundIdentifier):
        distanceToLeader     = msg.distanceToLeader
        currentEstimatedSize = msg.estimatedSize
        broadcastClusterMessage(
            clusterIdentifier       = myClusterIdentifier,
            roundIdentifier         = msg.roundIdentifier,
            senderIdentifier        = myNodeIdentifier,
            distanceToLeader        = distanceToLeader + 1,
            estimatedSize           = currentEstimatedSize,
            sizeContribution        = localSizeAccumulator,
            receiverIdentifier      = msg.senderIdentifier,
            radiusContribution      = localRadiusAccumulator,
            receiverMaximumDistance = distanceToLeader
        )
        resetReceiveTimer()
        localSizeAccumulator   = 1
        localRadiusAccumulator = distanceToLeader

To modify this code for the non-ID case, you would

• Keep track of the number of closer nodes you hear from within a round, then use that number to divide the sizeContribution when broadcasting.
• Check if you have the correct number of hops to receive the msg.sizeContribution (identical to the radius estimation) instead of checking that we are the intended recipient.

A remaining issue

We solved the issue when a small cluster joins and changes a big cluster’s ID, but not when a small cluster leaves a larger cluster and takes the leader with it, causing the larger cluster to change ID. Preferably, if a smaller cluster splits from a larger one, it should be the smaller one that must pick a new ID.

This issue might be mitigated if the leader node is migrated towards a central position in the swarm, either physically or logically. An example might be to have the leadership role passed to a neighbor if that neighbor has more neighbors than you do (higher degree centrality). Another option may be to have nodes identify themselves as edge nodes if they have a hop-count equal to the farthest seen hop-count (my first idea was to identify edge nodes by those that don’t have any neighbors who are farther from the leader than they are, but this happens to include a lot of nodes that are not on the edge, see if you can tell why). If we can identify edge nodes, then we can have every node calculate how far it is from the nearest edge node in the same way the radius metric was calculated, and then move the leadership role to nodes with a farther distance to edge nodes.

But this is for another time.