Peer to Peer Chat Network in Go (6)

This will be a list of interesting modifications you can make to the code in response to some security concerns.

A quick overview of public keys

A person can generate a pair of keys, a private key and public key. The private key is never shared, while the public key everyone knows. The two keys are linked such that anything encrypted with the public key can only be decrypted using the linked private key. You can also generate signatures for data using a private key, which the public key can be used to verify (which allows people to confirm they hold a private key without actually sharing the private key itself).

Security Concerns

Can’t verify sender

Currently when someone sends a message, they fill out a username field to indicate who the message is from. Nothing stops a malicious actor from using someone else’s username on their own message, thus impersonating them.

In order to stop this, we will require everyone sign their messages. This means instead of usernames, they will have public keys. When we receive a message with pubic key (now our username/identifier), the message must carry with it a signature generated by the associated private key. The recipient can then use the public key to verify the signature, thus proving the message was sent by the user with that public key. If we wanted to impersonate that user, we would need to be able to provide a valid signature, which we can’t do without the private key.

This does leave us with the issue of a readable username since public keys are not human readable. This is a difficult issue. If we allow people to define arbitrary usernames, and we display the usernames instead of keys, then people can copy usernames without copying private keys. We would need a way to communicate to the recipient that messages with the same username may not be from the same person. We could attach to all usernames a snippet of the users public key, but that again is not human readable, and people could still be fooled (similar to phishing emails with addresses similar to a trusted source, or a fake website like “welIsfargo.com”, did you notice one of the l’s was an i?). A good solution is to have recipients define for themselves a persons contact information. On first contact, people will only see the public address, but they can create an address book to map public keys to names, which will be used from that point on. This is how texting on our phones work, which is why we rarely see a scam where people attempt to impersonate someone in your address book, they can’t (although they can pretend to have a new phone, or a similar excuse for not already being in your contacts).

We still want some security for first contact (or for people who never add an address to their contacts), a good compromise will be to display a snippet of the public key, long enough so that it can’t be impersonated, but short enough not to clutter up the screen. A string of 40 characters will give us 320 bits, which is more then enough for our purposes.

But a longer key may not always be safer, here are some thoughts on readability vs security.

The main security concern with identity is that someone will impersonate another person. In order to “solve” this, we have given everyone a long key that only they have (the chance of another person generating the same key is practically zero), which can be used to identify them. But humans are lazy and don’t spend much time making absolutely certain that something is correct. This means the security of the key is not necessarily proportional to its length.

Imagine if we made the key 100 digits long, not only would it take up too much space on the screen, but people may ignore it entirely, ruining the purpose of the long key in the first place. Even 10 digits may be too long for people to track, but here we can leverage some understanding of our monkey brains. If we take the 10 digits and represent them on screen in a more human readable form, they become more secure. So perhaps you represent a user by one of 100 unique avatars and 10 unique colors (3 digits used) in one of 100 frames of 10 potential colors (3 more digits), then the last 4 digits you just print below as two alphanumeric symbols. People are much more likely to notice if a color changes, or avatar changes, or one of the symbols change, making the key more secure. Visually you can imagine the embedding space of all possible keys, then a box/sphere/other shape around your key that represents how “similar” a key has to be in order to fool people. The size of this shape can shrink depending on what representation of the key you choose. Because of how our brains seem to operate, you are forced to make a trade-off between the shapes’ number of dimensions and width, all to try and minimize the percent of space the shape takes up.

Replay attacks

Even though people can no longer impersonate each other, they can record a message someone sent and send it again later. Imagine someone keeps track of every message you’ve ever sent, now although they can’t create new messages with your signature, they have a lot of messages to choose from which are signed by you. After they’ve recorded enough of your messages, they might as well have your signature too for all the good it does.

In order to solve this problem we use the same solution we used to solve the infinite message passing in the flood-fill network. By adding a number only used once (nonce) to each message, people will know when a message has been sent twice and ignore it the second time (notice this is identical to the flood fill network packets, and if we hadn’t separated the network logic and chat logic, we could just use the nonce already there, but we also would have had to move all the other security measures there as well). Make sure the nonce is used in signing, otherwise people can take your signed message and just change the nonce, creating a still valid message that is susceptible to replay attacks.

Messages content and recipient are visible

We have the ability to directly send messages, but right now the content is entirely visible, ruining the purpose of direct messaging. A clever idea is to encrypt the content of the data using the recipients public key, then only they are able to decrypt it with their private key. This actually solves three problems at once, hiding the content, recipient, and sender of the message. By encrypting the message we already encode the recipient to whom the message is meant. If you can decrypt the message, then it is for you, if you can’t, then it is not. We can also hide the sender by encrypting the entire message, including the sender. Absolutely no one except the recipient will know who sent the message (whom they also verify by the message signature).

Message sender is visible

Although it seems we just solved the issue of hiding the sender, there is another way in which the origin of a message can be found. If an adversary controls a significant percentage of the network, they can track the spread of a message, including the first time a message is seen. If the adversary has a connection to the originator of a message, then they can immediately tell where in the network the message started. If the adversary can have just one connection to every node, they will be able to tell for every message exactly who sent it. This means if nodes have on average 5 connections, then an adversary only needs to make up 20% of the network in order to mostly correctly identify the sender of any message. As the number of average connections goes up, the necessary percentage of ownership goes down.

To solve this problem we will have each message first take some random hops through the network before flood filling. The originator will choose a random number between 0 and 10, then send it only over a single connection, then the next person will decrement the number and again pass it over a single random connection, repeating until the number hits 0 and the node begins the flood fill. This means the adversary cannot use the “center” of the flood fill to locate the sender since the sender didn’t initiate the flood fill. The only way the adversary can now identify the origin of a message is to control every single connection out of the sender to see its initial hop. This means not only does an attacker need to control almost the entire network, they have to own more as the number of connections per node increases, not the other way around.

DDoS

A flood-fill network is the least efficient design for message passing, a message gets unnecessarily sent N*(D-1) times, where N is the number of nodes and D is the average connection count. An attacker can take advantage of this inefficiency by overwhelming the network by simply generating lots of traffic, which will cripple every node in the network. You may realize on consideration of this problem that a solution is not obvious.

Any traffic generated by an adversary will quickly spread and be again generated by every node on the network. As an individual node we only have access to our immediate connections, so we can’t tell if anomalous traffic coming from one of our connections C is generated by C, or being passed along by C, so we don’t know if they are the adversary or not. Perhaps we track for anomalous traffic not by node, but by the signer of a message? But we face two issues with this solution: We would have to get rid of anonymous senders, and worse, adversaries can easily generate new public keys to send the crippling traffic from, avoiding our detection altogether.

An inconvenient solution is to impose a price on every message sent. The easiest form of this is to require “proof of work” on each message. Proof of work is easiest implemented using a hash function and a nonce. A sender would have to find the right nonce such that the hash of the combined message and nonce satisfies some requirement, such as the binary representation of the hash is greater then some number. As the requirement becomes more restrictive (in this case the number the hash must be greater then grows), the amount of nonces a user has to try increases, requiring more computation/time. You could require the difficulty of the proof of work to be proportional to the size of your message, so small messages cost little, while large messages cost more. This would stop attackers from saturating the network (unless they have vast amounts of computation).

Code

Below is the chat application using all of the mentioned modifications except the initial random hops, this is left as an exercise for the reader. A note: The user never actually sees another users public key since it is too long, so we store the mapping from the address snippet the user does see to the full address, then replace it when necessary in the background.

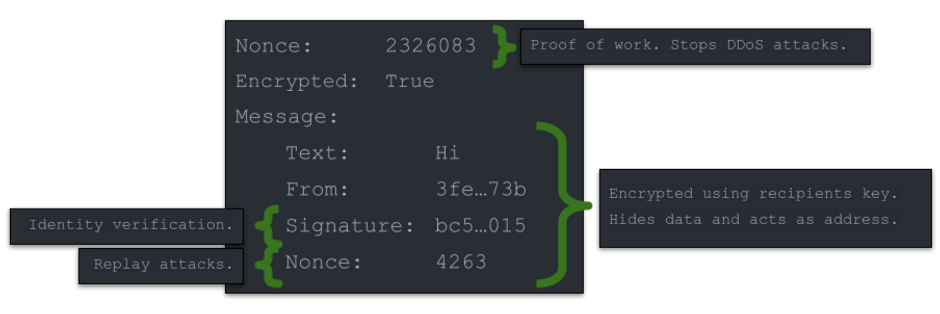
Here is an overview of the message construction.

Choosing the difficulty for the proof of work

The hash function essentially returns a random number between $0$ and $2^{256}$. The requirement is that our hash is greater than some difficulty level $D$. How many hashes do we expect to try before our condition is met? A little thinking brings us to the answer $\frac{2^{256}}{2^{256}-D}$. This is a function that approaches infinity as $D$ approaches $2^{256}$, which is not what we want. Our desire is for the expected time $E[T]$ to be proportional to the size of the message $L$. Using very simple algebra we can find $E[T]=\frac{2^{256}}{2^{256}-D}=L$ implies that $D=2^{256}(1-\frac{1}{L})$. But we may also want to require some work for even very small messages, this way an attacker can’t spam the network with lots of tiny messages (we solved what you might think of as a bandwidth attack, but we want to prevent latency attacks to). Solving this is now straightforward. To add an additional $A$ amount of time for each message, we solve $E[T]=\frac{2^{256}}{2^{256}-D}=L+A$ to get $D=2^{256}(1-\frac{1}{L+A})$. In the code we set $A = 124$, and multiply $L$ by $64$. This means for a message of length $1000$ we expect the user to look through $1000\times 64+124=64124$ hashes.

Whats neat about this is that when $A=0$, sending 1 message of size $S$ takes the same amount of time as sending 10 messages of size $\frac{S}{10}$. Another way of looking at it is that people pay a cost exactly proportional to the message size they want to send. When $A \ne 0$, then we introduce an additional cost exactly proportional to the number of messages they send.

Files

The floodnet library has not changed, so below are the only two files that are different/new.

package main

import (
	"P2PChatTutorial6/floodnet"
	"bufio"
	"encoding/json"
	"fmt"
	"math/rand"
	"os"
	"strings"
	"time"
)

type WorkedMessage struct {
	Nonce     int
	Encrypted bool
	Message   []byte // may or may not be encrypted
}

type Message struct {
	Text      string
	From      []byte
	Signature []byte
	Nonce     int
}

type Contact struct {
	name    string
	address []byte
}

var network *floodnet.Network
var addressBook map[string]Contact  // from short address to contact
var seenAddresses map[string][]byte // track recent seen address. From short address to full address
var seenMessages map[int]bool       // stops replay attacks

func main() {
	rand.Seed(time.Now().UnixNano())
	generateSignature()

	addressBook = make(map[string]Contact)
	seenAddresses = make(map[string][]byte)
	seenMessages = make(map[int]bool)

	// use default network address, or get network address from command line arguments
	entryAddress := "[::]:55555"
	if len(os.Args) > 1 {
		entryAddress = os.Args[1]
	}

	network = floodnet.NewNetwork(entryAddress)

	go handleNetwork(network)

	reader := bufio.NewReader(os.Stdin)
	running := true
	for running {
		// get text from terminal input
		text, err := reader.ReadString('\n')
		if err != nil {
			fmt.Println(err)
			break
		}
		text = strings.TrimSpace(text)

		// check if the user wants to quit
		if text == "exit" || text == "quit" {
			running = false
		} else if text == "add contact" { // check if user wants to add a contact
			fmt.Print("> Address to place in contacts: ")
			text, err := reader.ReadString('\n')
			if err != nil {
				fmt.Println(err)
				continue
			}
			shortAddress := strings.TrimSpace(text)

			fullAddress, ok := seenAddresses[shortAddress]
			if !ok {
				fmt.Print("> Address has not been seen")
				continue
			}

			fmt.Print("> Contacts new name: ")
			text, err = reader.ReadString('\n')
			if err != nil {
				fmt.Println(err)
				continue
			}
			username := strings.TrimSpace(text)
			addressBook[shortAddress] = Contact{name: username, address: fullAddress}
			fmt.Printf("> Added %s to contacts as %s\n", shortAddress, username)
		} else { // user wants to send a message
			// get our public key
			from, err := exportRsaPublicKeyAsPemBytes(&privateKey.PublicKey)
			if err != nil {
				fmt.Println(err)
				continue
			}

			workedMessage := &WorkedMessage{}
			message := &Message{Text: text, From: from, Nonce: rand.Int()}
			directMessage := false
			var recipient Contact

			// check if this is a direct message
			if text[0] == '@' {
				args := strings.Split(text, " ")
				if len(args[0]) == 1 {
					fmt.Println("> No address given")
					continue
				}
				if len(args) == 1 {
					fmt.Println("> No message given")
					continue
				}

				desiredRecipientName := args[0][1:]
				// search through known contacts for the given name
				desiredRecipient, found := Contact{}, false
				for _, contact := range addressBook {
					if desiredRecipientName == contact.name {
						desiredRecipient = contact
						found = true
					}
				}
				if !found {
					fmt.Println("> No contact with that address in the address book")
					continue
				}
				recipient = desiredRecipient
				directMessage = true
				message.Text = text[len(args[0]):] // make sure to chop off receivers username from the message
			}

			// sign the message
			err = signMessage(message)
			if err != nil {
				fmt.Println("Error signing the message:")
				fmt.Println(err)
				continue
			}

			// get byte representation to either send or encrypt
			messageJSON, err := json.Marshal(message)
			if err != nil {
				fmt.Println("Error encoding the message:")
				fmt.Println(err)
				continue
			}

			// encrypt if direct messaging
			if directMessage {
				workedMessage.Encrypted = true
				workedMessage.Message, err = encryptMessage(messageJSON, recipient.address)
				if err != nil {
					fmt.Println("Error encrypting the message:")
					fmt.Println(err)
					continue
				}
			} else {
				workedMessage.Message = messageJSON
			}

			// do proof of work
			doProofOfWork(workedMessage)

			// send out message
			workedMessageJSON, err := json.Marshal(workedMessage)
			if err != nil {
				fmt.Println("Error decoding the worked message:")
				fmt.Println(err)
				continue
			}
			network.Write(workedMessageJSON)
		}
	}
}

func handleNetwork(network *floodnet.Network) {
	running := true
	for running {
		encoded := network.Read() // blocking until we receive a workedMessage
		workedMessage := &WorkedMessage{}
		err := json.Unmarshal(encoded, workedMessage) // byte array to message struct
		if err != nil {
			fmt.Println("Error decoding the worked message:")
			fmt.Println(err)
			continue
		}

		// check proof of work
		if !verifyProofOfWork(workedMessage) {
			fmt.Println("Received message with invalid proof of work")
			continue
		}

		message := &Message{}

		// decrypt if encrypted
		if workedMessage.Encrypted {
			messageDecrypted, err := decryptMessage(workedMessage.Message)
			if err != nil {
				// if we can't decrypt, the message is not for us, ignore
				continue
			}
			workedMessage.Message = messageDecrypted
		}

		// decode message
		err = json.Unmarshal(workedMessage.Message, message)
		if err != nil {
			fmt.Println("Error decoding the message:")
			fmt.Println(err)
			continue
		}

		// check we haven't already seen this message
		if seenMessages[message.Nonce] {
			continue
		}

		// verify signature
		if !verifySignature(*message) {
			fmt.Println("Received message with invalid signature")
			continue
		}

		// passed all checks, let user see the message
		displayName := string(message.From[100:140]) // the entire public key would take up the screen
		if storedName, ok := addressBook[displayName]; ok {
			displayName = storedName.name
		} else {
			seenAddresses[displayName] = message.From // store for later if we want to create a contact for this person
		}
		if workedMessage.Encrypted {
			fmt.Printf("%s ---> %s\n", displayName, message.Text)
		} else {
			fmt.Printf("%s -> %s\n", displayName, message.Text)
		}

		// track so replay attacks can't happen
		seenMessages[message.Nonce] = true
	}
}  

package main

import (
	"crypto"
	"crypto/rand"
	"crypto/rsa"
	"crypto/sha256"
	"crypto/x509"
	"encoding/binary"
	"encoding/json"
	"encoding/pem"
	"errors"
	"fmt"
	"hash"
	"io"
	"math"
)

var privateKey *rsa.PrivateKey

func generateSignature() {
	potentialKey, err := rsa.GenerateKey(rand.Reader, 4096)
	if err != nil {
		fmt.Println(err)
		return
	}
	privateKey = potentialKey
}

func verifySignature(message Message) bool {
	publicKey, err := parseRsaPublicKeyFromPemBytes(message.From)
	if err != nil {
		fmt.Println(err)
		return false
	}

	signature := message.Signature
	message.Signature = nil // make sure to zero out signature field
	encoded, err := json.Marshal(message)
	if err != nil {
		fmt.Println(err)
		return false
	}
	hashed := sha256.Sum256(encoded)

	return rsa.VerifyPKCS1v15(publicKey, crypto.SHA256, hashed[:], signature) == nil
}

func encryptMessage(message []byte, to []byte) ([]byte, error) {
	recipientKey, err := parseRsaPublicKeyFromPemBytes(to)
	if err != nil {
		return nil, err
	}

	return EncryptOAEP(sha256.New(), rand.Reader, recipientKey, message, nil)
}

func decryptMessage(message []byte) ([]byte, error) {
	return DecryptOAEP(sha256.New(), rand.Reader, privateKey, message, nil)
}

func signMessage(message *Message) error {
	// sign message
	message.Signature = nil // make sure to zero out signature field
	encoded, err := json.Marshal(message)
	if err != nil {
		return err
	}
	hashed := sha256.Sum256(encoded)

	signature, err := rsa.SignPKCS1v15(rand.Reader, privateKey, crypto.SHA256, hashed[:])
	if err != nil {
		return err
	}

	message.Signature = signature
	return nil
}

func verifyProofOfWork(workedMessage *WorkedMessage) bool {
	expectedHashAttempts := len(workedMessage.Message)*64 + 124
	difficulty := uint32(float64(math.MaxUint32) * (1.0 - 1.0/float64(expectedHashAttempts)))
	// hash the workedMessage and ensure it passes the difficulty
	encoded, err := json.Marshal(workedMessage)
	if err != nil {
		panic(err)
	}
	hash := sha256.Sum256(encoded)
	hashNum := binary.BigEndian.Uint32(hash[:])

	return hashNum > difficulty
}

func doProofOfWork(workedMessage *WorkedMessage) {
	// find a nonce until the requirement is satisfied
	for !verifyProofOfWork(workedMessage) {
		workedMessage.Nonce++
	}
}

func exportRsaPublicKeyAsPemBytes(pubkey *rsa.PublicKey) ([]byte, error) {
	pubkey_bytes, err := x509.MarshalPKIXPublicKey(pubkey)
	if err != nil {
		return nil, err
	}
	pubkey_pem := pem.EncodeToMemory(
		&pem.Block{
			Type:  "RSA PUBLIC KEY",
			Bytes: pubkey_bytes,
		},
	)

	return pubkey_pem, nil
}

func parseRsaPublicKeyFromPemBytes(pubPEM []byte) (*rsa.PublicKey, error) {
	block, _ := pem.Decode(pubPEM)
	if block == nil {
		return nil, errors.New("failed to parse PEM block containing the key")
	}

	pub, err := x509.ParsePKIXPublicKey(block.Bytes)
	if err != nil {
		return nil, err
	}

	switch pub := pub.(type) {
	case *rsa.PublicKey:
		return pub, nil
	default:
		break // fall through
	}
	return nil, errors.New("Key type is not RSA")
}

func EncryptOAEP(hash hash.Hash, random io.Reader, public *rsa.PublicKey, msg []byte, label []byte) ([]byte, error) {
	msgLen := len(msg)
	step := public.Size() - 2*hash.Size() - 2
	var encryptedBytes []byte

	for start := 0; start < msgLen; start += step {
		finish := start + step
		if finish > msgLen {
			finish = msgLen
		}

		encryptedBlockBytes, err := rsa.EncryptOAEP(hash, random, public, msg[start:finish], label)
		if err != nil {
			return nil, err
		}

		encryptedBytes = append(encryptedBytes, encryptedBlockBytes...)
	}

	return encryptedBytes, nil
}

func DecryptOAEP(hash hash.Hash, random io.Reader, private *rsa.PrivateKey, msg []byte, label []byte) ([]byte, error) {
	msgLen := len(msg)
	step := private.PublicKey.Size()
	var decryptedBytes []byte

	for start := 0; start < msgLen; start += step {
		finish := start + step
		if finish > msgLen {
			finish = msgLen
		}

		decryptedBlockBytes, err := rsa.DecryptOAEP(hash, random, private, msg[start:finish], label)
		if err != nil {
			return nil, err
		}

		decryptedBytes = append(decryptedBytes, decryptedBlockBytes...)
	}

	return decryptedBytes, nil
}  

And now try spinning up three instances the application. You should see everyone has an address instead of a name. You can then add that address into your contacts, changing the name in front of future messages. Adding a contact also allows you to directly message that person. A direct message received will be indicated with a longer arrow after the name. Below is an example interaction of three people.

$ ./chat
I am announcing a message!
F4vDtG/WgBaHapAo2k/OBDZG2Oc27VVLeOaK+FbQ -> I created a contact
F4vDtG/WgBaHapAo2k/OBDZG2Oc27VVLeOaK+FbQ --->  I have a secret to tell you
F4vDtG/WgBaHapAo2k/OBDZG2Oc27VVLeOaK+FbQ -> I told Adam a secret

$ ./chat
RrUQ/wYe6cI21ODgBi0aGTwYocqcWfzjn53fsZyO -> I am announcing a message!
add contact
> Address to place in contacts: RrUQ/wYe6cI21ODgBi0aGTwYocqcWfzjn53fsZyO
> Contacts new name: Adam
> Added RrUQ/wYe6cI21ODgBi0aGTwYocqcWfzjn53fsZyO to contacts as Adam
I created a contact
@Adam I have a secret to tell you
I told Adam a secret

$ ./chat
RrUQ/wYe6cI21ODgBi0aGTwYocqcWfzjn53fsZyO -> I am announcing a message!
F4vDtG/WgBaHapAo2k/OBDZG2Oc27VVLeOaK+FbQ -> I created a contact
F4vDtG/WgBaHapAo2k/OBDZG2Oc27VVLeOaK+FbQ -> I told Adam a secret

And we notice the secret message wasn’t seen by the third person. You can also now try to hack the system as the third person. You have access to all the messages announced in the network, and people could easily write their own malicious clients. See if you can break the security systems in place so the third person can read the secret message.

The only commands in this final application are:

• exit
• quit
• add contact
• @<a contacts name> <your message to that contact>
• <a message everyone will see>