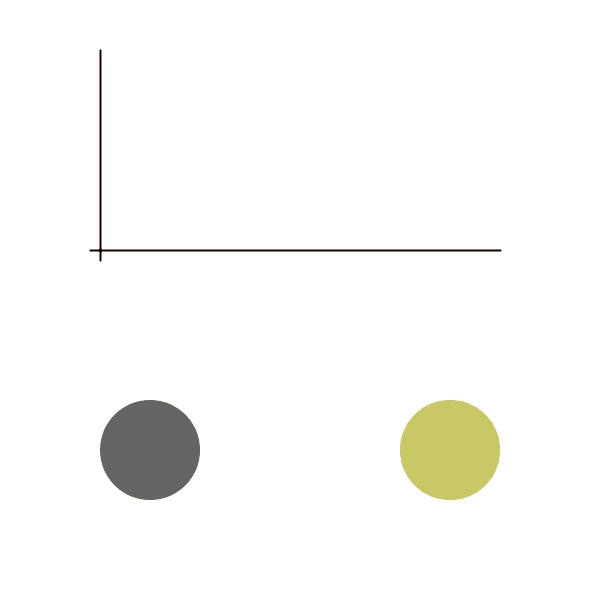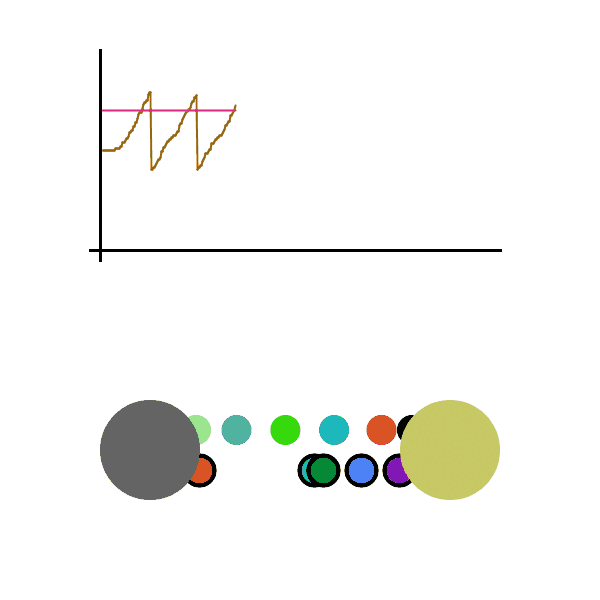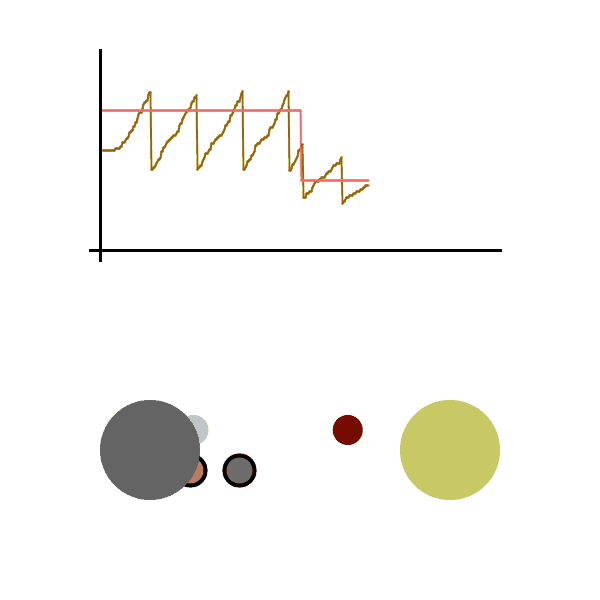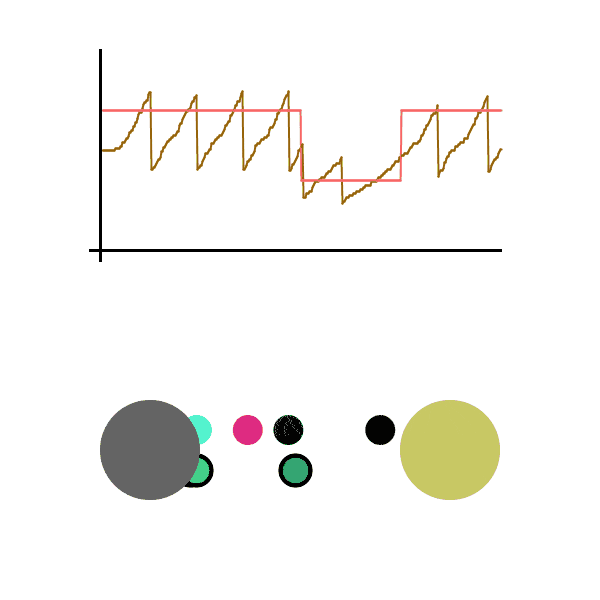Ants
One day a biologist is studying ants, then she notices that the ants stop leaving the nest when food becomes scarce. This seems obvious, that’s what they should be doing, but the tricky bit is how are they doing it? It’s not pheromones, and it’s not spatial coordination, but something far more clever.
Ants are a strange but fascinating family of insect species. Contrary to the image that a queen brings to mind, queens in ant colonies only produce workers, they don’t manage them. Most ant species only have a few casts, usually the worker, the queen, and males, but not a manager class. This means large swarms of ants need to work together without a top-down view, each ant knowing very little about the whole, while still functioning as a whole. So how do ants manage themselves? While there are many aspects of the ant colony that could be investigated (job allocation, building structures, effective foraging, and much more), we will look at the very specific task of determining how many ants should leave the nest to search for food.
I strongly suggest that before moving on, you attempt to figure this out for yourself. Create an algorithm that can run in every ant so that we get the following behavior: When there is a lot of food to return to the colony there should be a lot of ants foraging, and when food is scarce there should be few ants foraging. Keep in mind each ant does not know what other ants know, they can communicate only when they bump into each other. Once you have given it sufficient thought, read on. The solution is beautifully clever and simple.
Each ant will have an internal counter, this counter goes up when the ant sees another ant return to the colony with food, but the counter also slowly decreases over time. When this counter reaches some threshold, the ant leaves the colony to search for food. That’s it, that’s the entire mechanism. Let’s see how well this works.
Below we have some ants (red dots) that want to go outside to search for a pile of food (green dot). Each ant has a random threshold (gray bar), which when filled up, tells them when they should head out to search for food. The counter (green bar) is always decreasing but increases when an ant returns home with food. When an ant hits their threshold they leave the colony. We every so often tell an ant that they hit their threshold (even if they haven’t) so that there can be “exploratory ants”. You can increase an ants counter by clicking on it. If you click anywhere else, the food pile will grow. When the pile gets small, there is a greater chance the ant will not get food from the pile, this simulates the difficulty of finding food when it grows scarce.
We can see the number of ants exploring starts low, but increases to match the food available, then decreases as the food slowly dries up. This is amazing! This strategy should adapt to almost any circumstance. If the amount of food decreases, if the path becomes more difficult (it starts raining, an adversary/obstacle blocks the path, or the food moves farther away), if there are suddenly fewer ants to explore, regardless of the reason, the strategy is robust and will adapt. Not only all this, but the strategy should scale to almost any size. There are bounds obviously, depending on the specific circumstance, but in most general cases this strategy should work. A much more careful look at exactly how ants use this strategy and how to recreate it in simulation can be found in The Regulation of Ant Colony Foraging Activity without Spatial Information.
It is perhaps because of this robustness and scalability that we see this exact mechanism throughout nature and our own systems. The paper A feedback control principle common to several biological and engineered systems covers in more depth the concept talked about here, and how it’s seen in ant foraging, cell size, plasticity in the brain, TCP congestion control, and machine learning. We will finish by looking at how the same strategy used by the ants was unknowingly recreated for TCP congestion control.
The Internet
If you want to send a large file to someone, it needs to be broken up into small parts called packets. These packets have to travel across the internet, an environment entirely unknown to your computer. You might be on a computer connected to a phone hotpot, which connects to a cell tower, and then since you’re using a VPN, the packet first has to travel halfway around the world, and then to some company’s server room, which likely has its own internal routing. Or you might be directly connected by Ethernet to the computer you want to talk to. Your computer has no idea, so it doesn’t know how quickly it can send packets.
A computer wants to send packets efficiently, too fast and your losing packets, too slow and the task won’t be done as quickly as it could be. How can the computer determine how quickly to send these packets? Now is a good time to try and apply the trick the ants used for this problem. A necessary piece of information is that when a packet is received, an acknowledgment is sent back to the sender.
When the sender receives an acknowledgment, they increase their sending speed, and when they fail to get an acknowledgment they decrease the sending speed. This way when we aren’t sending packets fast enough we always get an acknowledgement back, so we keep increasing the sending speed. When we eventually send out too many packets, not all of them will get back, so we decrease the sending speed. We oscillate around the optimal sending speed, and will adapt to any network issues in real time! This is a simplification of what TCP does in its entirety, but you should now be able to understand its finer details.
One interesting detail is that TCP uses additive increases and multiplicative decreases. This means if we graph the sending speed over time, we will get a saw-tooth shape. There are two main reasons for this approach: this is the mathematically optimal solution (again, see A feedback control principle common to several biological and engineered systems), and sending too many packets is worse than sending too few packets.
A simulation can be helpful, here is a toy example of one person sending packets to another person. We graph the speed at which the sender sends out packets. When an acknowledgment is received, the speed increases additively, and when an acknowledgment fails to be seen, the speed is divided in half. The pink line is the maximum speed at which packets can be sent without any loss (usually not known since it depends on many independent variables in the network), above this line there’s an increasing chance that the packet is lost. The brown line is the speed at which the sender is sending packets.
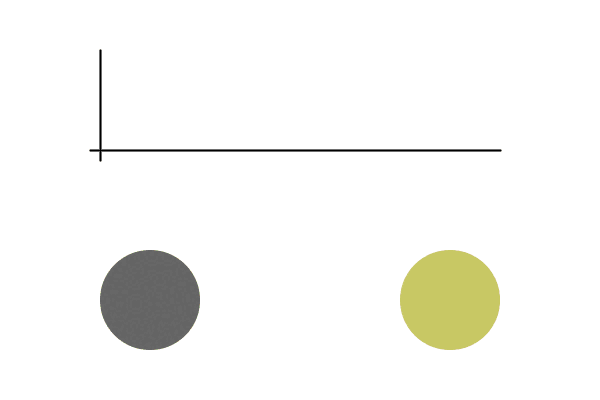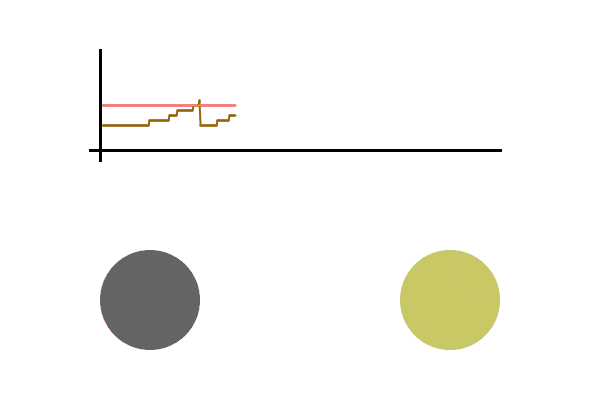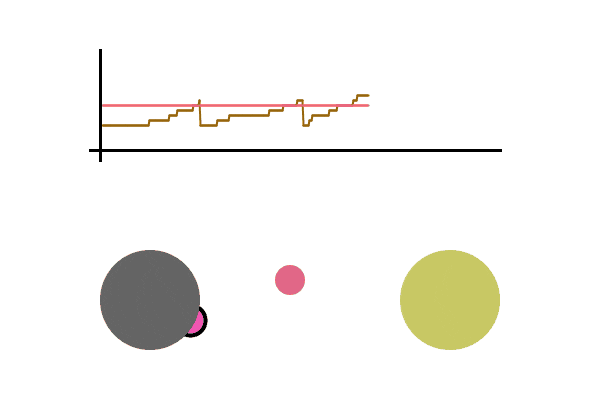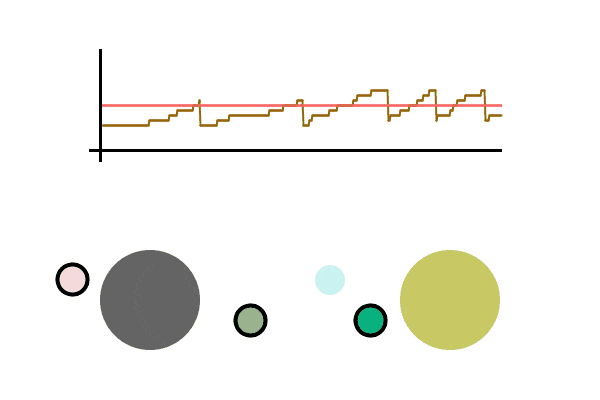
We see the graph bounce around the max sending speed, meaning the sender rarely loses a packet and is operating at near max efficiency. All this without actually knowing the conditions of the network. It should be able to quickly adapt to any network changes. Let’s run it again, this time sending packets much faster. Let’s also cause a disruption in the network while the file is being sent (seen as the pink line dropping), which is then fixed a second later.
The Sender was able to adapt to the brief network slowdown and adapt back when the network was fixed. The sender had no idea what was happening between themselves and the receiver, but adapted to it anyway.
While relatively simple, this control principle works remarkably well in being both robust and scalable in environments where discreet feedback is all you have. I hope you found this introduction interesting, definitively look at the links I provided earlier in order to learn more.