Simulated Economy (3)

Multiple Markets

Lets start with just two markets. We’ll have wood and chairs, with wood being used to build chairs. But first lets just look at the two markets uncoupled, each with personal values set at random. This will give us a baseline for what these markets look like when they aren’t influenced by each other. The number of owned goods by some actors are changed at points in time, this is to double check the market is still adapting to change in supply.

In order to couple these markets, we will give actors the ability to build a chair from the wood they have. But how do actors determine if they should use up some of their wood in order to build a chair? Imagine to build a chair you need to use up 4 wood. Further imagine you have 4 pieces of wood, the expected market value for each is \$2, you personally value each piece at \$3 (ignoring diminishing utility for now), the expected market price of a chair is \$16, and you personally value a new chair at \$10. The potential value of gaining a new chair would be \$16 since you know you would sell it rather then keep it. The value of keeping the wood would be \$12. So you would decide to use the wood to build a chair, generating a surplus of \$4. Another way of looking at this calculation would be to say the value of building a chair is \$4.

The value of gaining a new piece of wood would be \$3. If you have to choose between gaining a new piece of wood or building a chair, the best action would be to build a chair.

Every iteration we give actors the ability to choose between chopping wood (gaining 1 wood) or building a chair (losing 4 wood, gaining 1 chair). We quickly run into an issue though. Chairs and wood are continually being created, making them continually less valuable until they’re worth nothing. In order to resolve this we need a way for goods to leave the market. In this case we’ll have chairs break every once in a while. But the frequency of chairs breaking is important, if its too high (higher then the frequency that chairs are made) then any chair won’t last more then a few generations, if it’s too low (lower then the frequency that chairs are made) then chairs will flood the market until they are again worth nothing. We could set the frequency of chairs breaking equal to the frequency of chairs being made, but we want the frequency of chair building to adapt to the market, so this isn’t a viable solution. Lets turn to real markets, why don’t we see this issue there?

If you were given the option to either cut wood with an expected return of \$0.01 or make a chair for a return of \$0.04, which would you choose? The answer is neither, its not worth your time. We need actors to consider the value of doing nothing. Lets call the act of doing nothing leisure. If an actor values leisure at \$3 then they won’t choose to cut wood unless they expect it to make more then \$3. Wood will naturally level out at \$3, and similarly the chair at \$12. By simply considering the cost of leisure we fix the issue of workers over-saturating the market.

// we sometimes break a chair
if rand.Float64() < 0.01 {
	if actor.markets[CHAIR].ownedGoods > 0 {
		actor.markets[CHAIR].ownedGoods--
	}
}

// evaluate all your actions
doNothingValue := actor.potentialPersonalValue(LEISURE)

cutWoodValue := math.Max(actor.potentialPersonalValue(WOOD), actor.markets[WOOD].expectedMarketValue)

buildChairValue := 0.0
materialCount := 4
if actor.markets[WOOD].ownedGoods > materialCount {
	potentialChairValue := math.Max(actor.potentialPersonalValue(CHAIR), actor.markets[CHAIR].expectedMarketValue)
	materialValue := math.Max(actor.currentPersonalValue(WOOD), actor.markets[WOOD].expectedMarketValue) * float64(materialCount)
	buildChairValue = potentialChairValue - materialValue
}

// act out the best action
maxValueAction := math.Max(math.Max(doNothingValue, cutWoodValue), buildChairValue)
if maxValueAction == doNothingValue {
	actor.markets[LEISURE].ownedGoods++ // we value doing nothing less and less the more we do it (diminishing utility)
} else {
	if maxValueAction == cutWoodValue {
		actor.markets[WOOD].ownedGoods++
	} else if maxValueAction == buildChairValue {
		actor.markets[WOOD].ownedGoods -= materialCount
		actor.markets[CHAIR].ownedGoods++
	}
	actor.markets[LEISURE].ownedGoods = 0 // make sure we have renewed value for doing nothing since we just did something
}

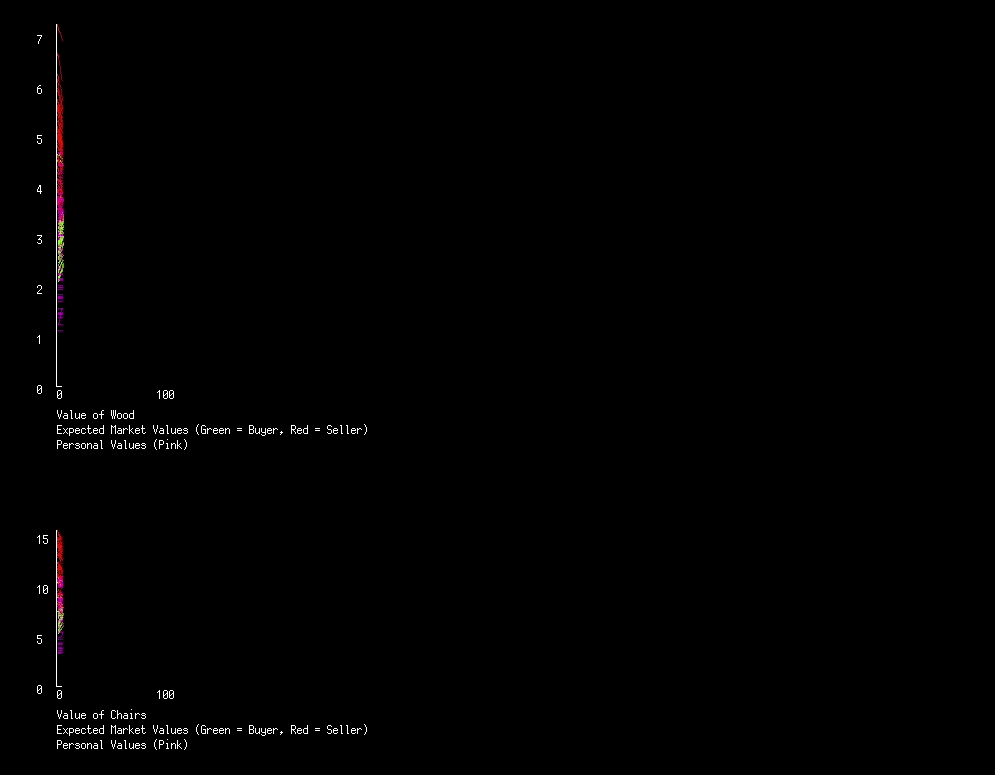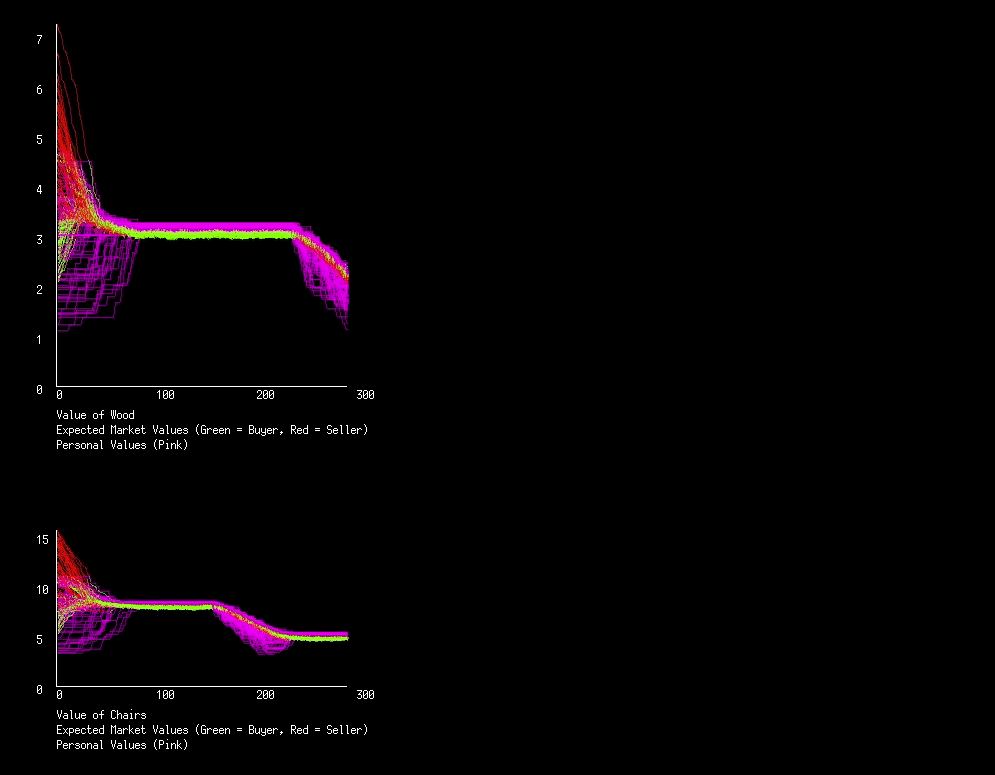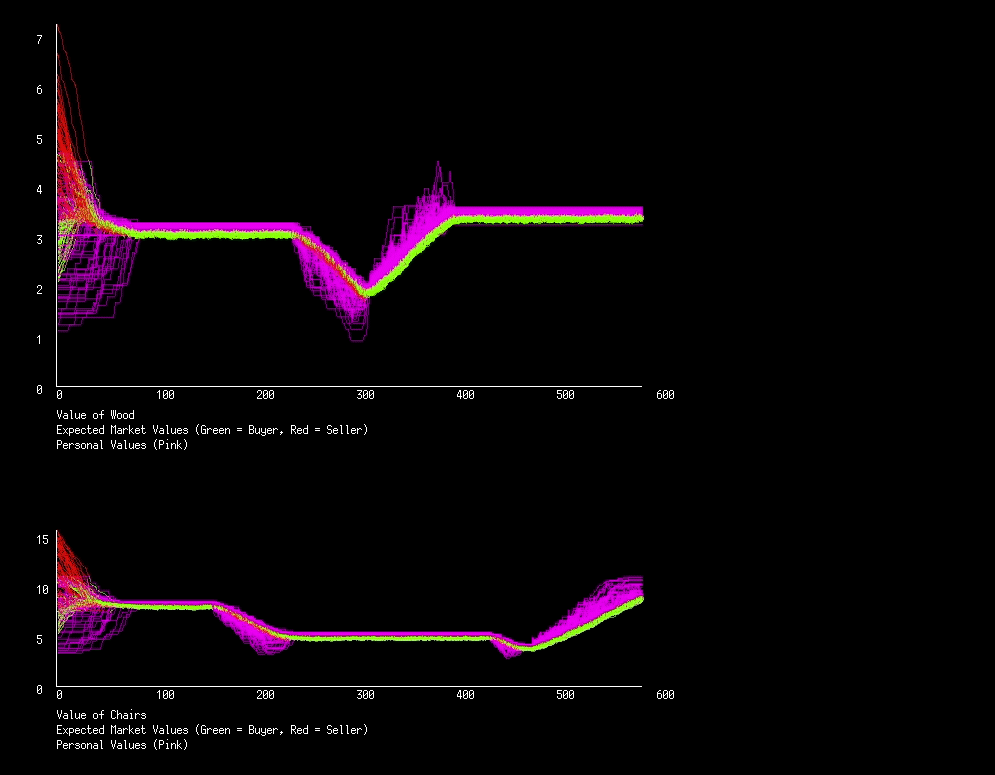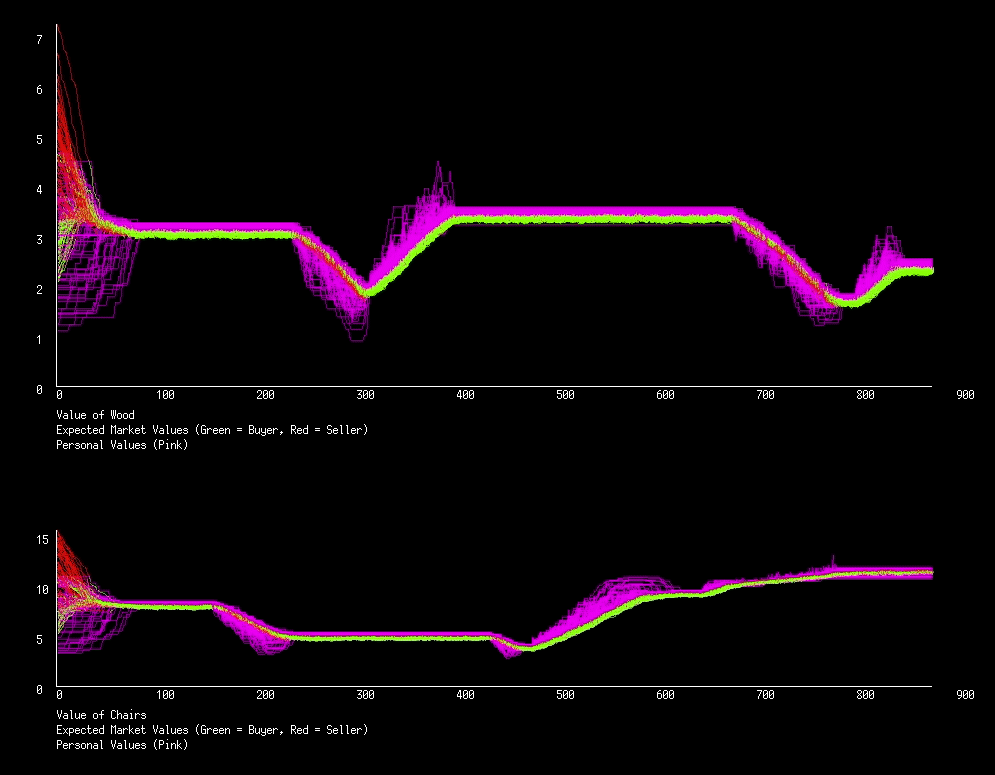
Below is the graph of value for both markets using the above code. Nothing too exciting is happening in this economy, but lets take a look at why the personal values (pink lines) look the way they do.

Lets look at the chairs. Initially everyone has a different personal value for a chair, but very quickly everyone has the same personal value, why? There’s never any communication of this value, so its not immediately obvious how everyone converges. What’s happening is that those who value a good more then others will buy, decreasing their personal value for that good, this is diminishing utility in action. Similarly, those that value a good less then others will sell until their personal value equals the expected market value.

So what about all the pink on top of the green line (the expected market value lines)? This is again due to diminishing utility. When a chair breaks, a person will suddenly value a chair more then they did, which we see as a bump in the pink line. And when someone builds a chair they loose multiple pieces of wood, so the actor suddenly values wood more then they previously did. At least once every iteration someone breaks or builds a chair, so every iteration a pink line bumps up, and we end up with a continuous wall of pink.

Messing With Markets

Lets poke different aspects of the markets and see what happens.

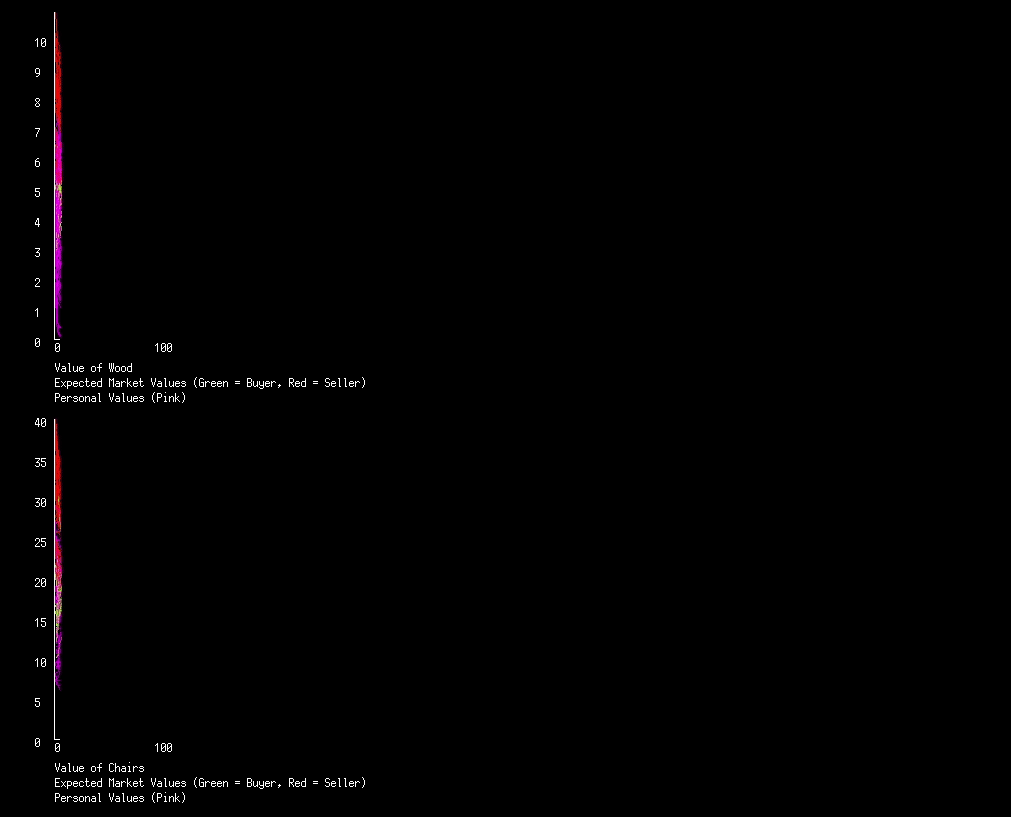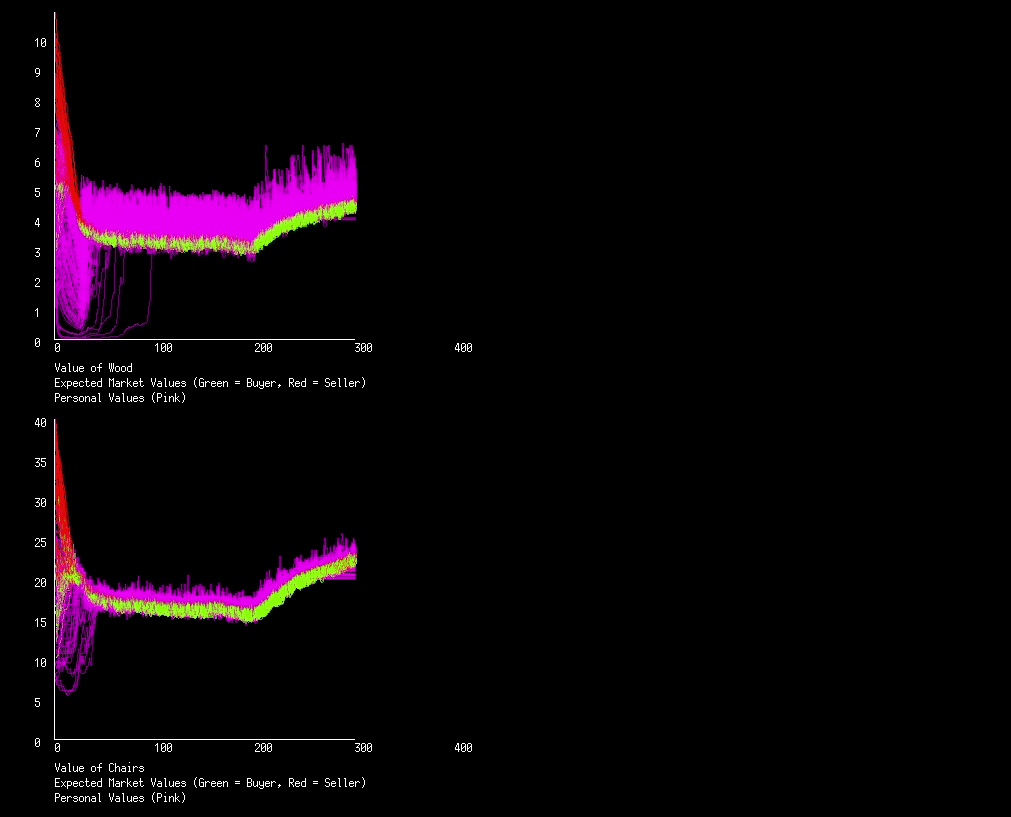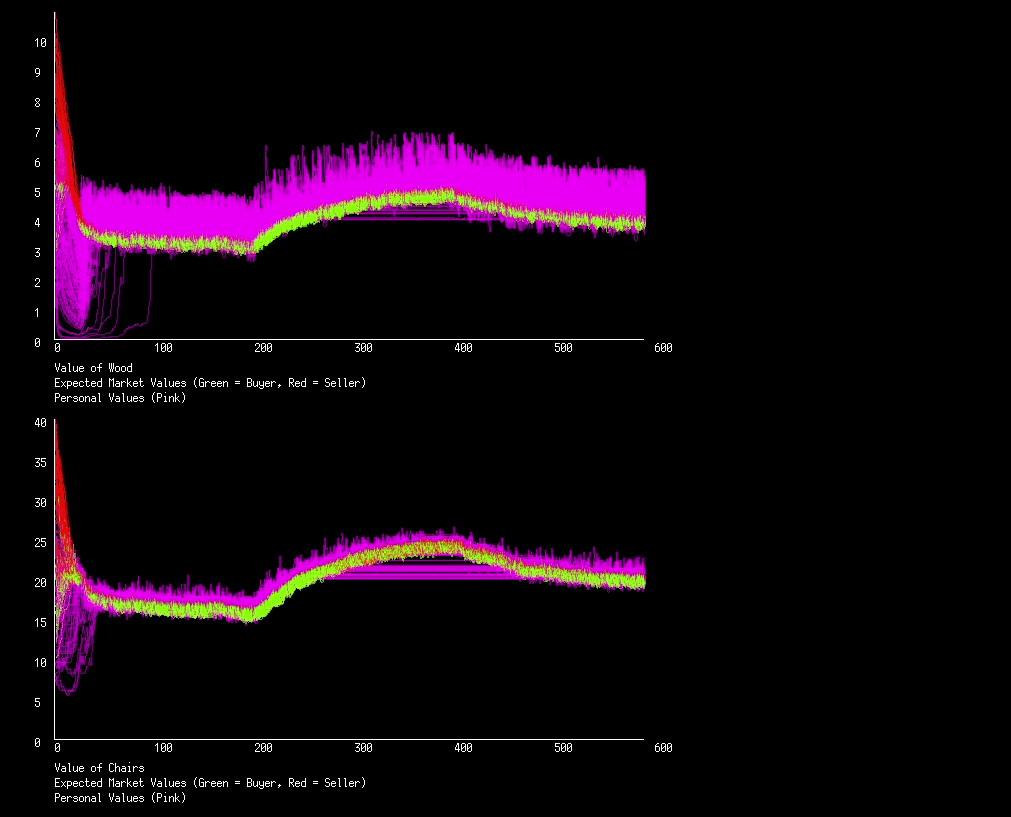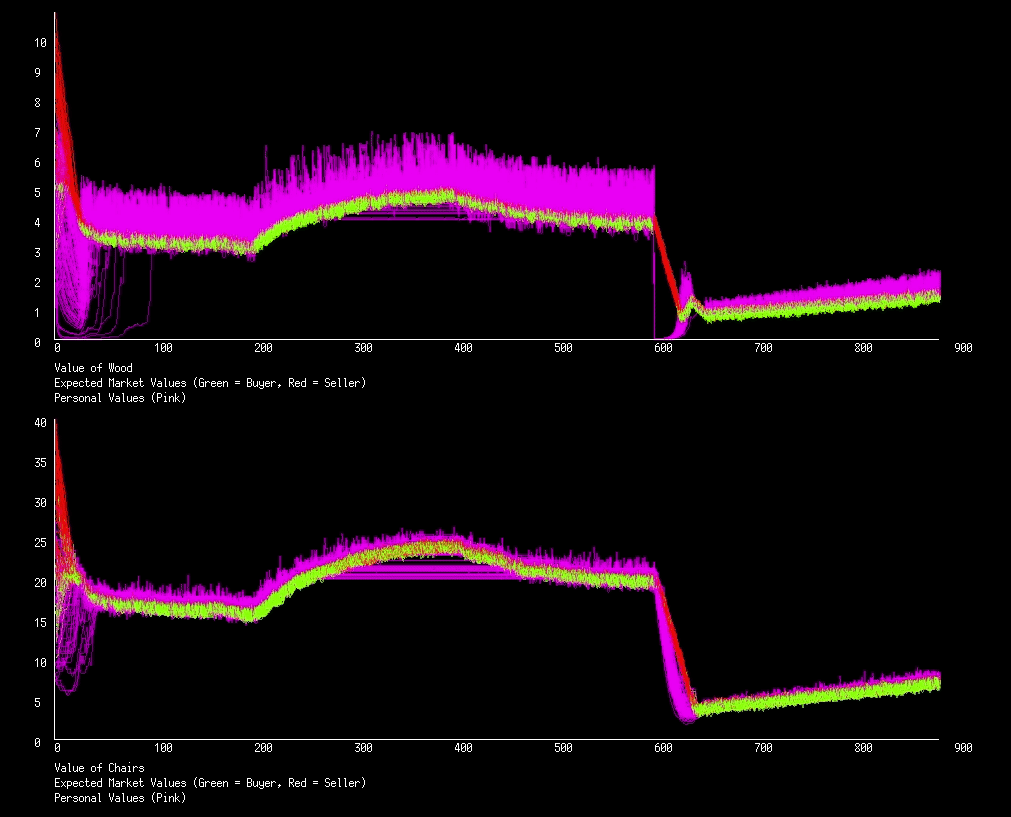
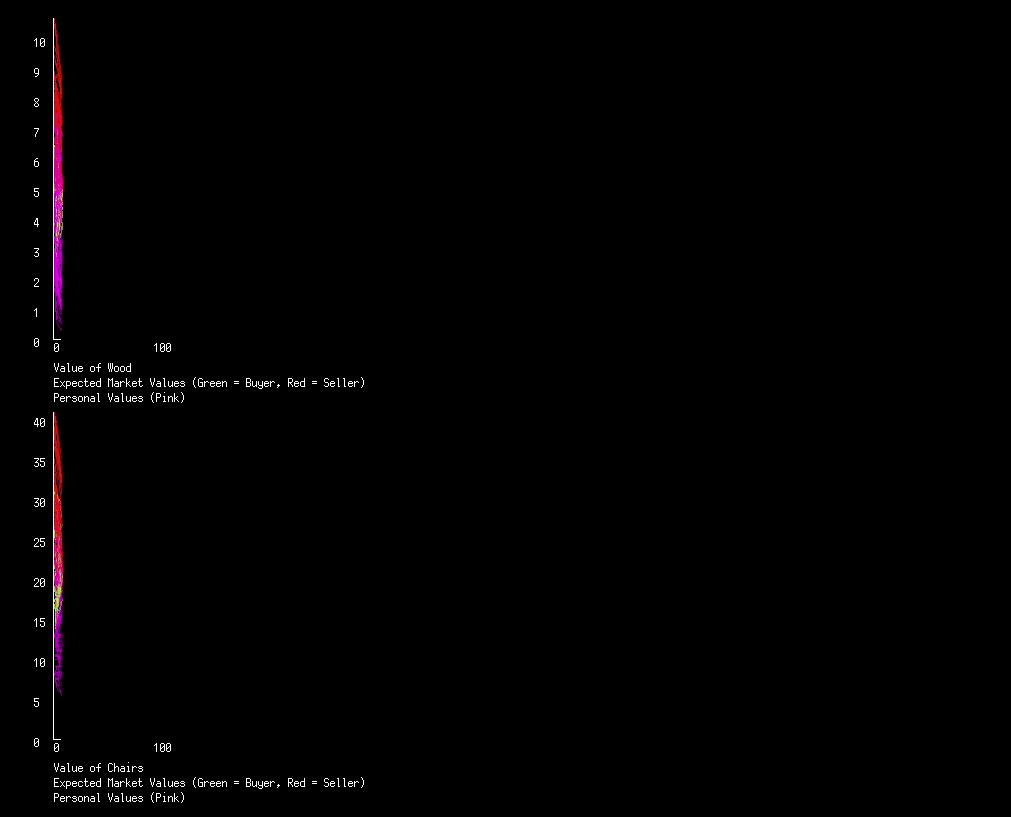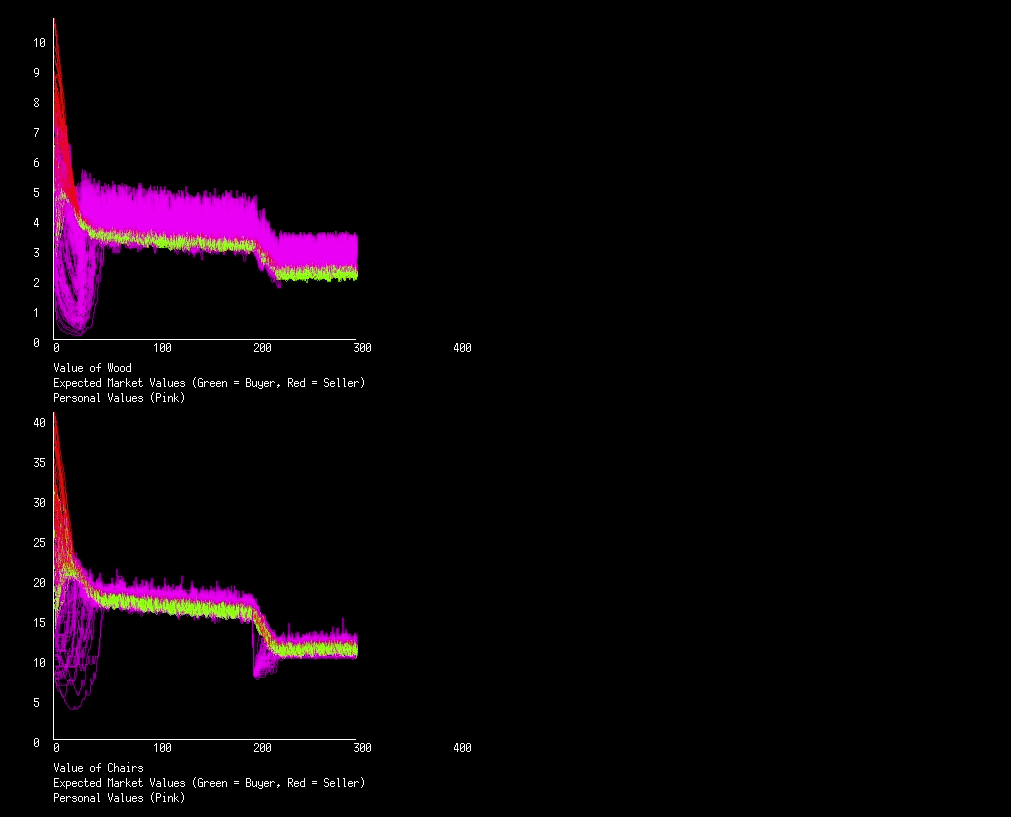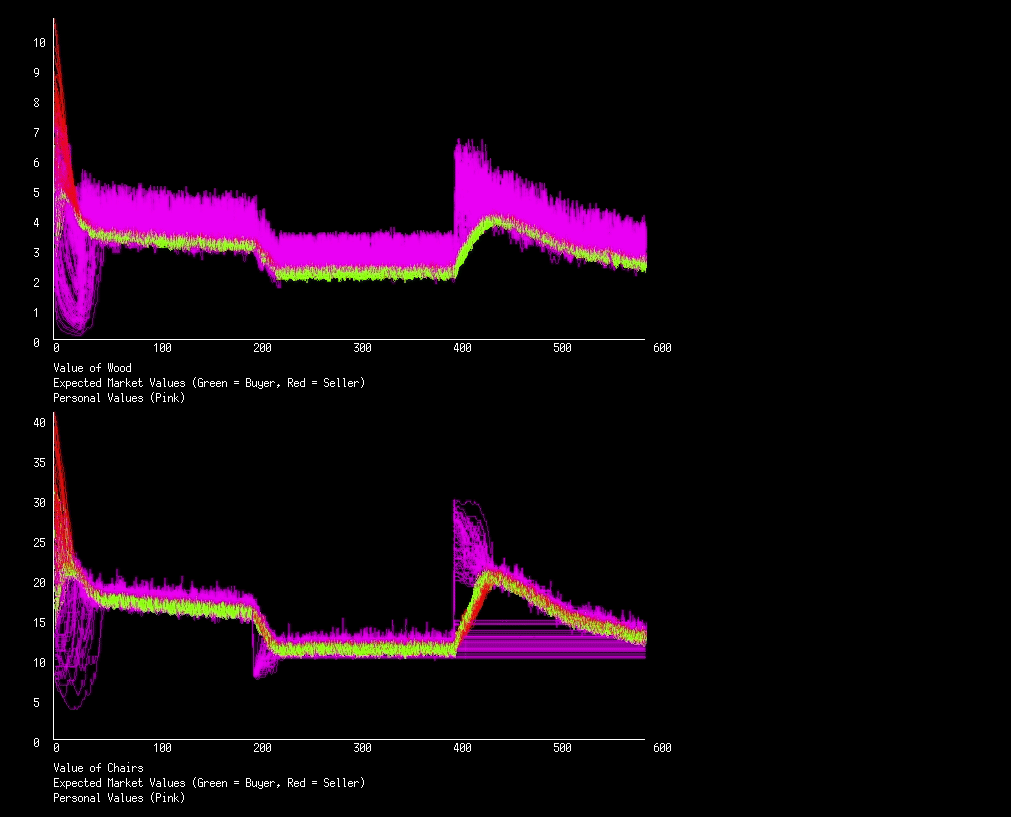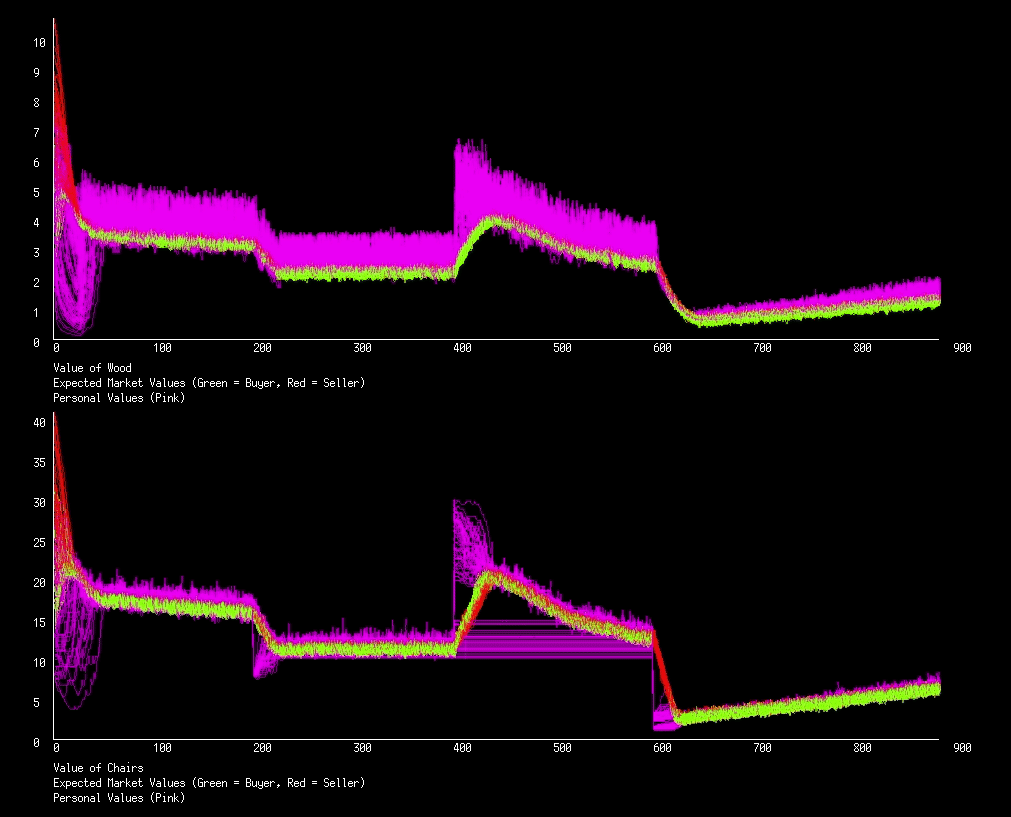
Lets start by having termites in iteration 200 to 400. Termites will randomly destroy pieces of wood each iteration, making it more scarce. At iteration 600 let’s have a new forest open for forestation, providing everyone with an overabundance of wood (an extra 100 pieces).

We see that when the termites were introduced, wood became more expensive, and excitingly, the chairs along with it. And when the termites left, both wood and chairs started to sink back to their normal values. We do notice some pink lines in both markets that stopped travelling with the green lines during the termite season, why is that? An actor has a maximum value for a good that they will ever pay (when they don’t have any of that good). When we start seeing these perfectly straight pink lines we will know that some actors have hit their price limit.

When the forest is opened up and the market has a sudden influx of wood, we see the prices drop dramatically, then very slowly increase (except for that blip at iteration ~610, what is that?). This is because with the influx of wood, two things happen: An actors personal value for wood will drop essentially to zero, so no one will buy, eventually lowering the price to match demand; and lots of really cheap wood will be used to make normal priced chairs, flooding the market, lowering the price of chairs. With the price of wood and chairs so low, people usually choose to relax instead. But chairs are slowly breaking, so their price slowly rises, and with it the price of wood.

Now lets influence the chair market and see how it impacts the wood market. We will have three events: at iteration 200 the actors will suddenly stop liking chairs so much due to a news article that correlates sitting with less money; at iteration 400 the government responds to the article by implementing a 1 chair policy, but just for a day, afterward people are free to build and buy more chairs; at iteration 600 the article is recalled and the government is forced to provide reparations, everyone gets 30 chairs.

And again we see the coupling of markets. When people stop liking chairs so much, the price of both chairs and wood drops. When people are restricted to a single chair they value both chairs and wood more. When everyone gets lots of chairs we see the same behavior as when everyone got lots of wood, a steep drop in price followed by a slow return to normal prices.

We now have multiple markets which are simply but intimately coupled, where an influence on one market influences the other. The issue of too many goods entering or leaving the market was solved by considering the value of leisure, then having each actor choose only the most valuable action available. Full repository is here.

Next

Currently the unit of value for goods are dollars, but this is unrealistic. If we were to double the amount of money everyone has, the price of goods would increase, but its value would stay the same (then decrease because diminishing utility kicks in when everyone is buying). We want inflation in our markets, and in order to do that we need to separate the concept of value and price.